Capítulo 4 Resultados

4.1 Modelando la cobertura de copa

4.1.1 Variables dependientes

El proceso de selección de las variables a incluir en los modelos inicia con la inspección visual de las distribuciones bivariadas de las candidatas a predictores. Se busca identificar las variables correlacionadas entre sí para evitar incluir información redundante en los modelos. En la figura 4.1 se explora las relaciones entre las variables de población (número de personas en un SU con una condición específica). La matriz triangular superior muestra los coeficientes de correlación de Pearson, la diagonal contiene el histograma de frecuencias de la variable y la matriz triangular inferior muestra un gráfico de dispersión y la línea de tendencia usando un modelo lineal entre cada par de variables. Es notoria la alta correlación entre población con ningún estudio y tener alguna limitación física ($\simeq 0.88$); pertenecer a una comunidad afrodescendiente y carecer de estudios ($\simeq0.92$) o ser afrodescendiente y tener alguna limitación ($\simeq0.88$). Esto representa una suma de condiciones desfavorables relacionadas entre sí, que desde el punto de vista del modelo sólo podrán ser representadas por la variable que mejor se relacione con la cobertura de copa y evitar así colinealidad entre los predictores.

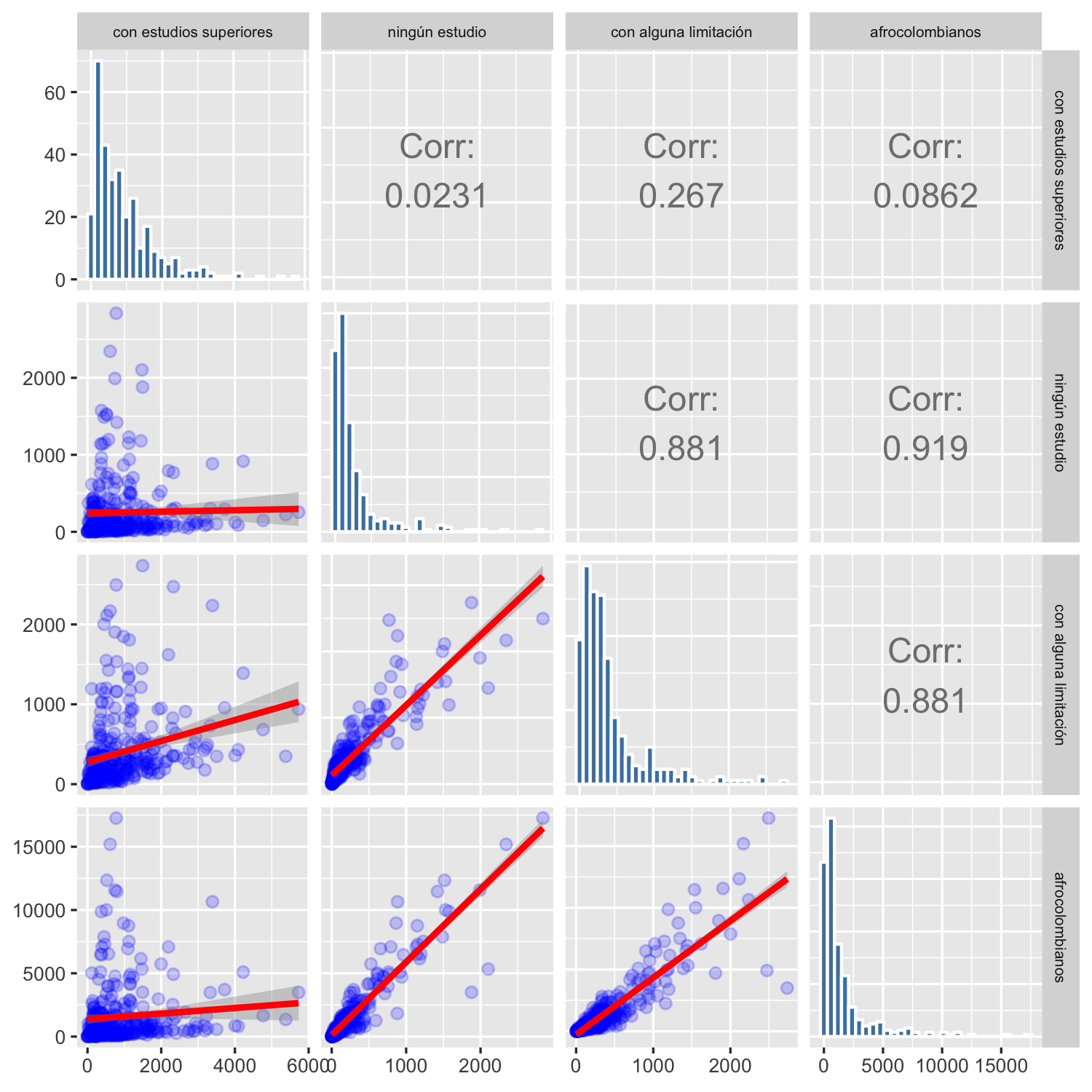
Figura 4.1: Comparación por pares entre predictores de población

Las mismas variables expresadas como porcentaje de la población de un SU muestran patrones similares (ver figura 4.2): existe una alta correlación negativa entre el porcentaje de población afro de un sector y la tenencia de estudios superiores ($\simeq-0.71$), una fuerte asociación positiva entre el porcentaje de personas afro de un sector y el porcentaje de personas que carecen de estudios ($\simeq 0.68$). También hay una fuerte relación inversa entre el porcentaje de personas de un sector sin estudios y el porcentaje de ellos que tiene estudios superiores ($\simeq-0.8$). Estos resultados refuerzan la concentración de condiciones desfavorables para la población explicadas por la condición racial.

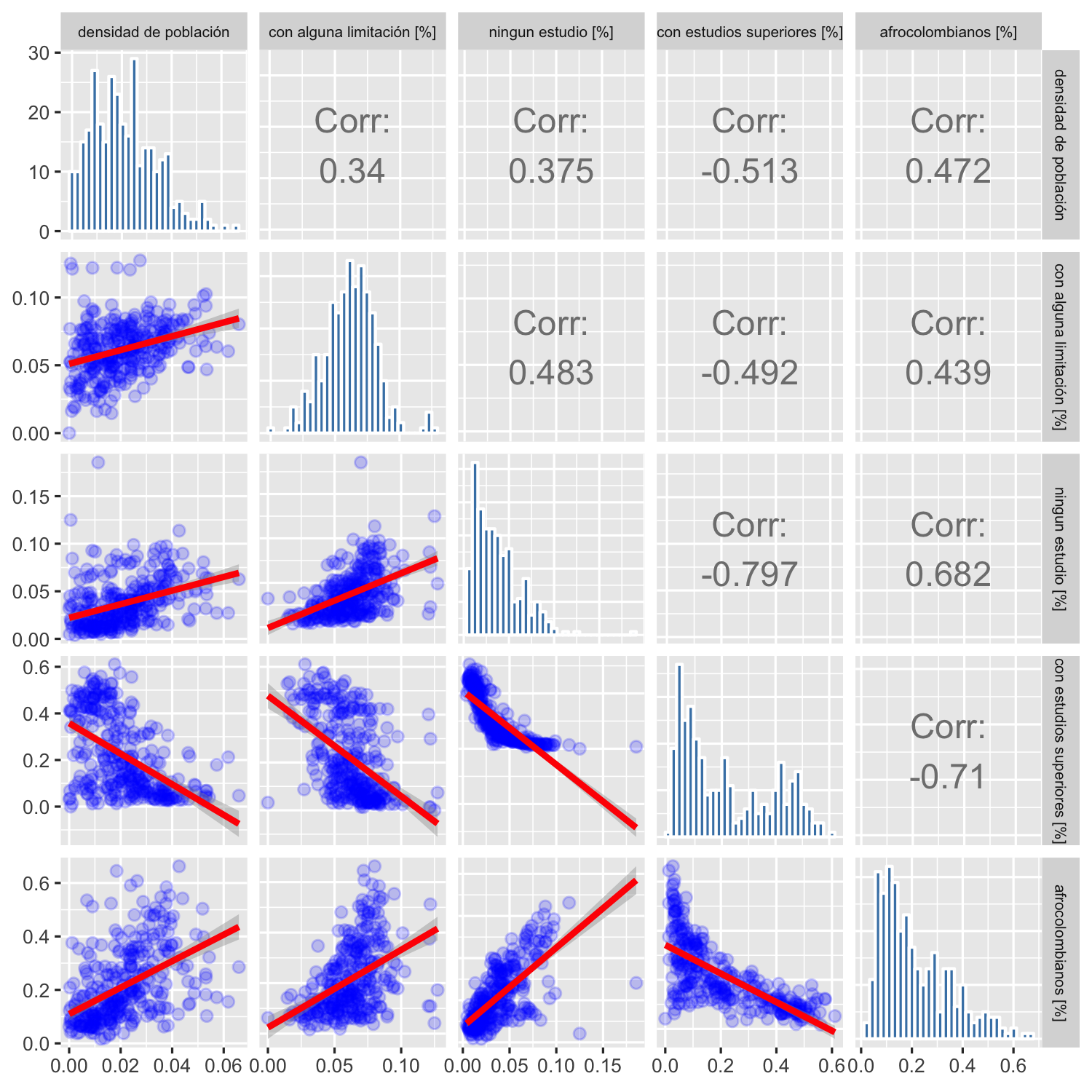
Figura 4.2: Comparación por pares entre predictores de población porcentuales

Los gráficos de azulejos son una forma resumida para consultar la intensidad de estas relaciones (figura 4.3) lineales entre las variables dependientes usando el coeficiente de correlación de Pearson, y las no lineales mediante el coeficiente de Spearman (figura 4.4).

Con base en los coeficientes de correlación de Pearson (figura 4.5) y Spearman (figura 4.6) entre las variables dependientes e independientes, y teniendo en cuenta las restricciones de colinealidad entre las variables dependientes, se seleccionaron las siguientes variables para los modelos lineales:

Para el área de copa (area_copa) los predictores seleccionados son: con estudios superiores, densidad de población, con alguna limitación [%], afrocolombianos [%].
Para la cobertura de copa (cobertura_copa.ap) los predictores seleccionados son: con estudios superiores [%], densidad de población, con alguna limitación [%], afrocolombianos [%]

Para la selección de variables sobre uso de los predios, los tipos de vivienda y área de espacio público se aplicó el mismo proceso. Para el área de copa se seleccionaron el área de espacios verdes y el porcentaje de viviendas tipo cuarto. Para el modelo de porcentaje de cobertura se seleccionaron el porcentaje de viviendas tipo apartamento, el porcentaje de viviendas tipo cuarto y porcentaje de área de espacios verdes.

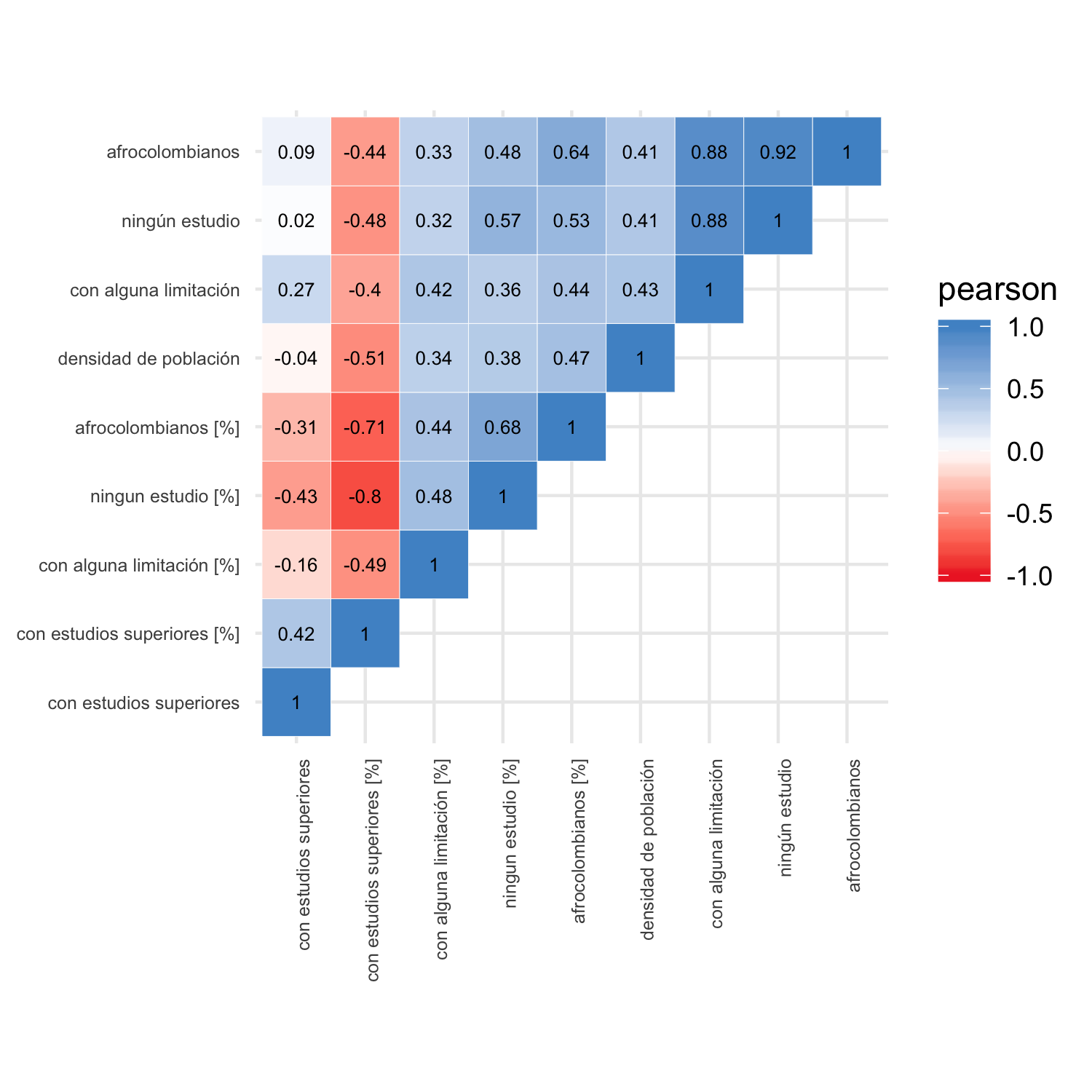
Figura 4.3: Coeficiente Pearson entre variables de población

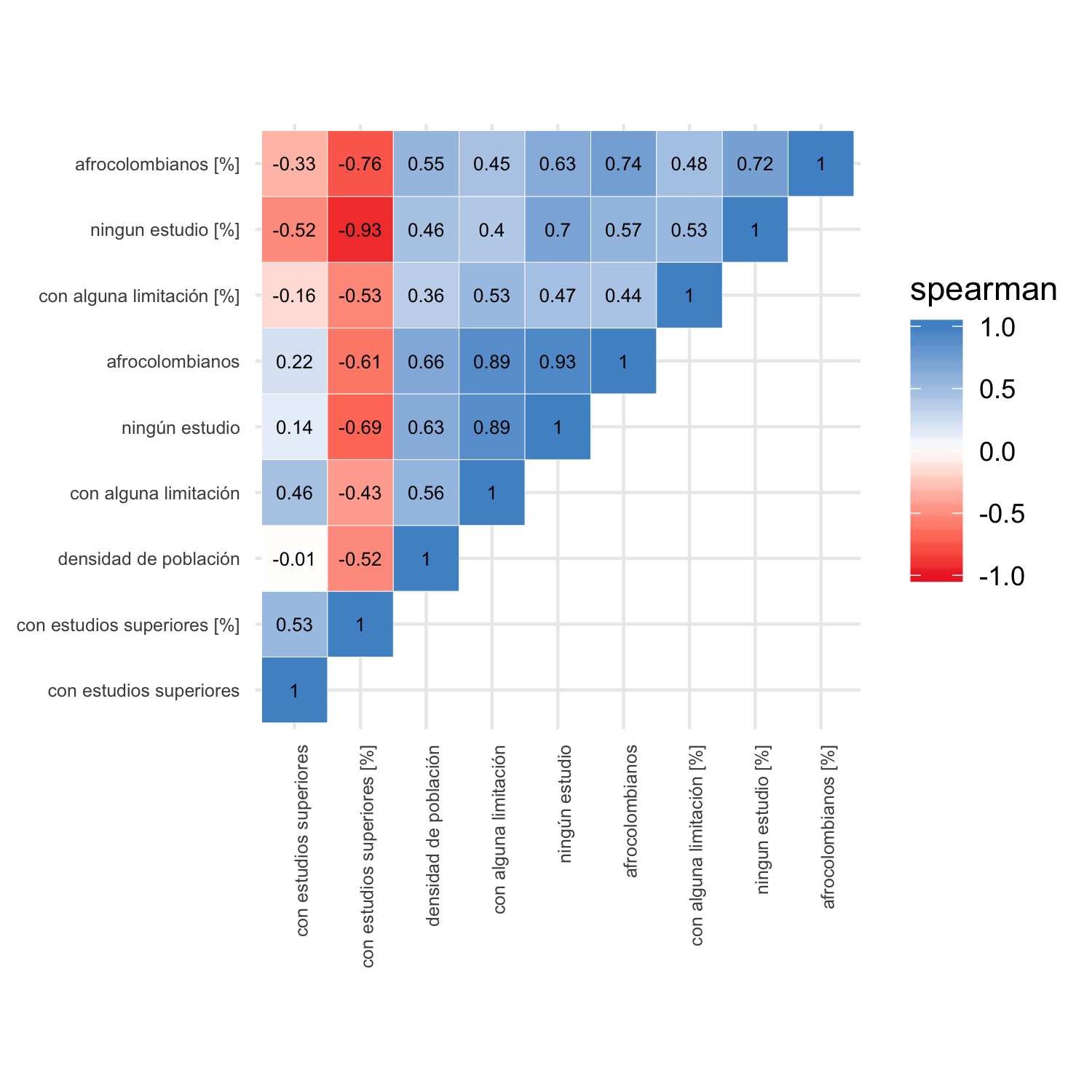
Figura 4.4: Coeficiente Spearman entre variables de población

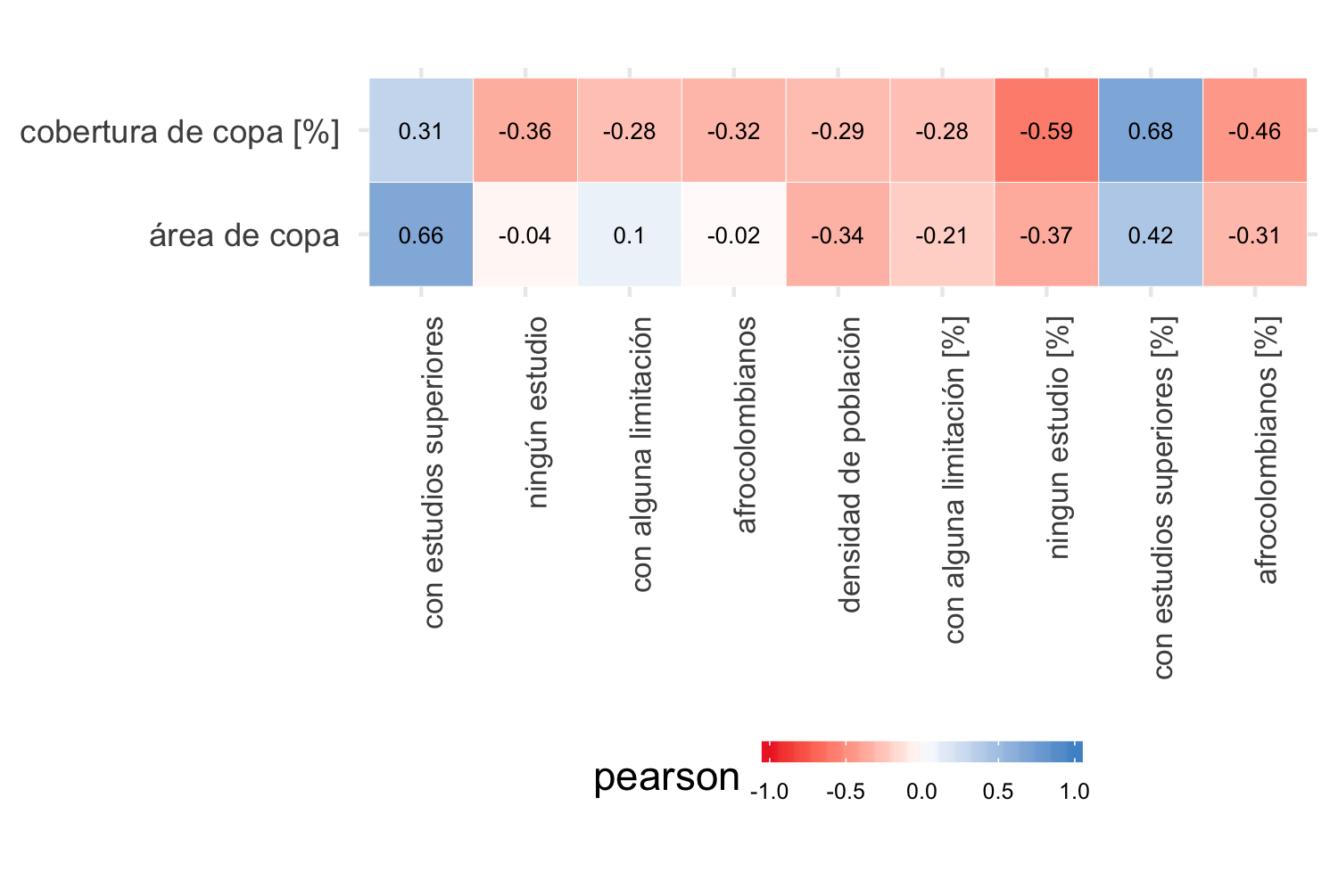
Figura 4.5: Coeficiente Pearson entre cobertura de copa y variables de población

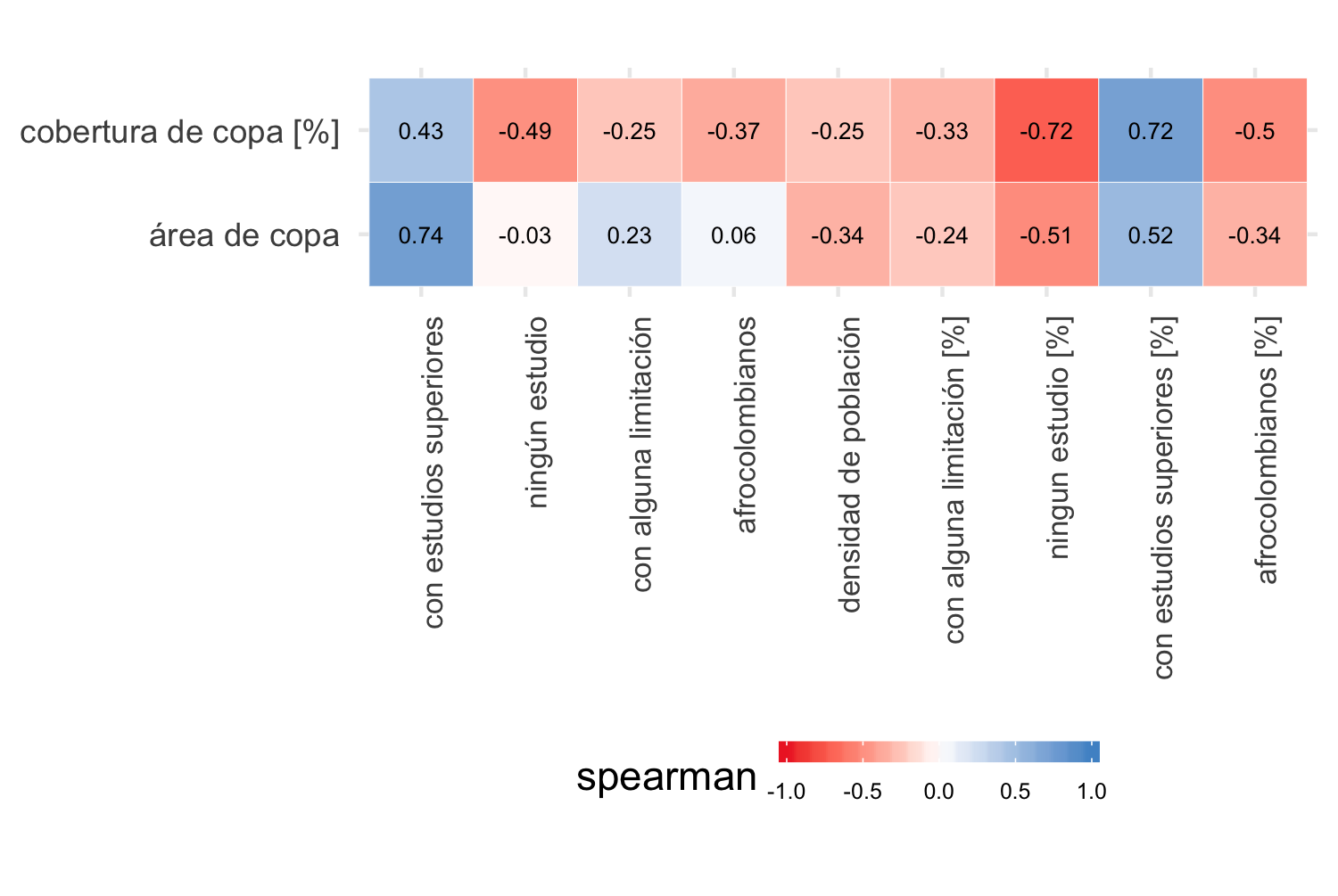
Figura 4.6: Coeficiente Spearman entre cobertura de copa y variables de población

4.1.2 Modelos de regresión lineal AU

Antes de evaluar los modelos se aplicaron varias transformaciones en busca de normalizar las distribuciones de las variables dependientes. Las que mejor resultado arrojaron en la formulación de los modelos fueron la transformación logarítmica para el caso del área de copa y la variable sin transformar en el caso de la cobertura de copa.

La tabla 4.1 resume los coeficientes de la regresión para el área de copa, la tabla 4.2 resume los coeficientes de la regresión para la cobertura de copa, y la tabla 4.3 resume las métricas de ajuste de ambos modelos.

Sin embargo, el ajuste de ambos modelos tiene media de los residuos muy cercanas a 0, al igual que el error cuadrático medio (MSE). En el caso del área de copa se obtiene un adjR-square de 60.5%, que es aceptable. Las variables significativas para el área de copa son: con estudios superiores, densidad de población, vivienda tipo cuarto [%], área de EV. Los resultados confirman que al nivel de toda el área de estudio, las condiciones de acceso a la educación de la población, la densidad de población, el tipo de vivienda y la disponibilidad de EV se correlaciona con el acceso a servicios ambientales del AU.

Para la cobertura de copa la única variable significativa es con estudios superiores [%]. Este único indicador porcentual, que hace una descripción local y comparable entre los SU, explica el 45.7% de la variabilidad de los datos, reforzando la importancia del indicador de acceso a educación superior como predictor del acceso a servicios ambientales del AU.

Para la siguientes fases se ignoraron las variables no significativas de los modelos lineales.

Tabla 4.1: Coeficientes OLS de área de copa - Log(AC)
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	0.788	0.013	62.256	0.000
con estudios superiores	0.312	0.024	13.013	0.000
densidad de población	-0.146	0.020	-7.283	0.000
con alguna limitación [%]	-0.020	0.025	-0.813	0.417
afrocolombianos [%]	0.010	0.021	0.481	0.631
vivienda tipo cuarto [%]	-0.145	0.030	-4.754	0.000
área de EV	0.119	0.028	4.310	0.000

Tabla 4.2: Coeficientes OLS de cobertura de copa - (CC)
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	0.03438	0.03989	0.86174	0.38948
con estudios superiores [%]	0.38210	0.04227	9.03961	0.00000
densidad de población	0.05573	0.03750	1.48613	0.13824
con alguna limitación [%]	0.05848	0.04470	1.30827	0.19173
afrocolombianos [%]	-0.02170	0.04410	-0.49201	0.62306
vivienda tipo apartamento [%]	-0.04561	0.03547	-1.28581	0.19945
vivienda tipo cuarto [%]	-0.06197	0.06163	-1.00545	0.31545
área de EV [%]	0.03971	0.03796	1.04619	0.29627

Tabla 4.3: Resumen métricas de ajuste OLS para el área de copa (AC) y cobertura de copa (CC)
medidasfit	Log(AC)	%CC
Shapiro-Wilk	0.98196	0.90416
SW p-value	0.00043	0.00000
Breusch-Pagan	21.62587	19.67634
BP p-value	0.00142	0.00631
Media Residuos	0.00000	0.00000
MSE	0.00345	0.01071
adj-Rsquare	0.60479	0.45931
AIC	-901.82032	-532.26094
Log likelihood	458.91016	275.13047

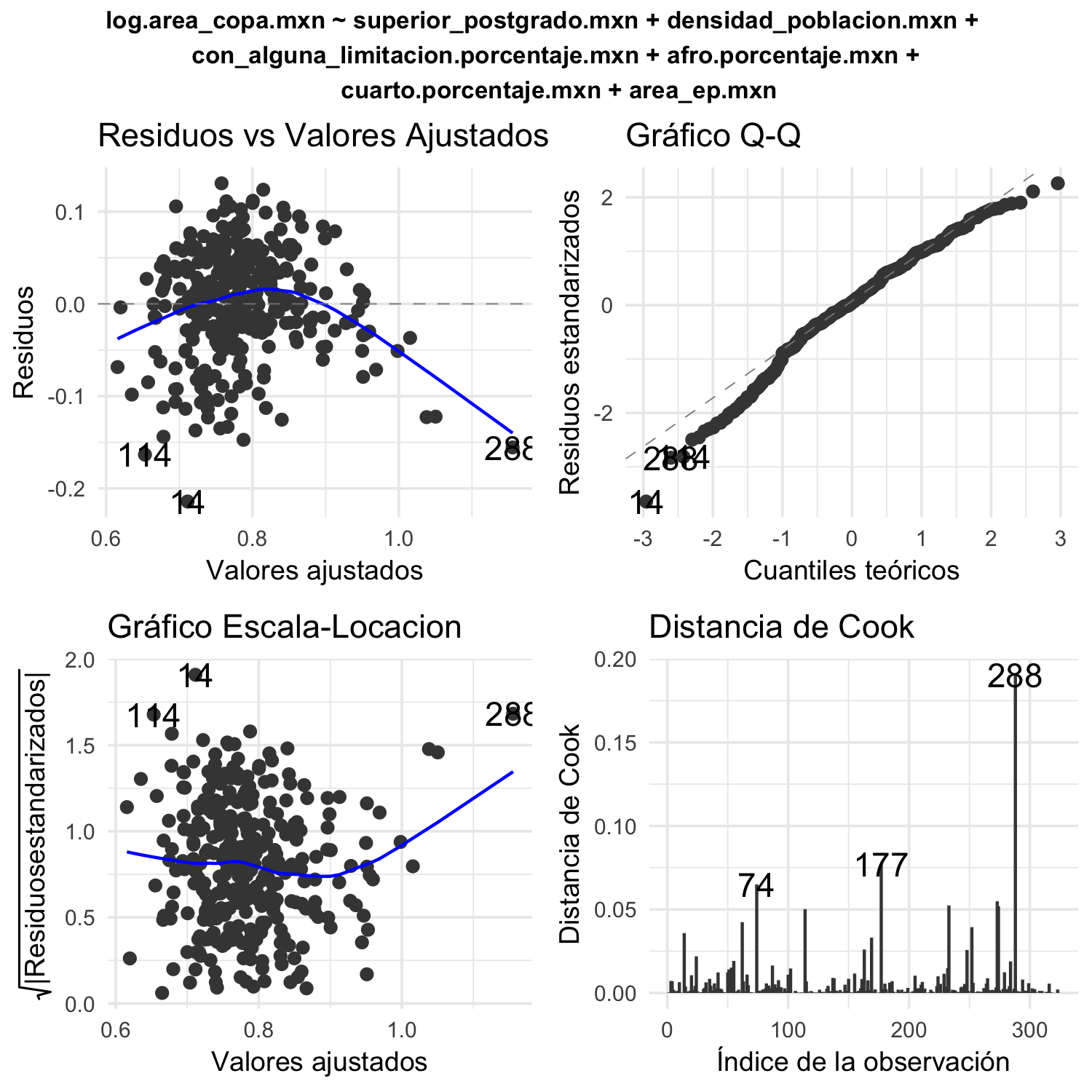
Figura 4.7: Gráficas diagnósticas para el análisis de regresión lineal de área de copa

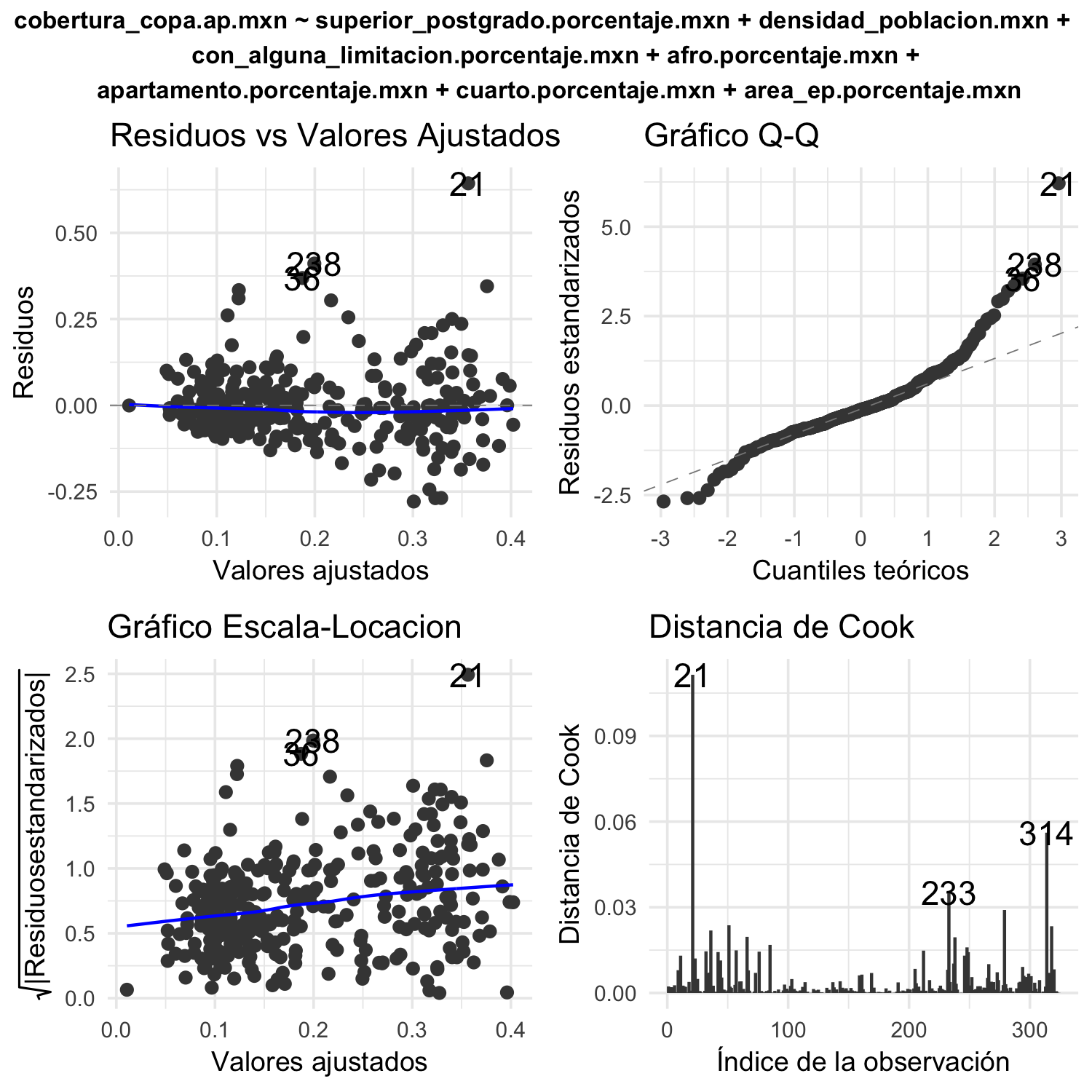
Figura 4.8: Gráficas diagnósticas para el análisis de regresión lineal de porcentaje de cobertura de copa

4.1.3 Modelado espacial AU

Las matrices de vecindad construidas para el análisis espacial son la queen $W_q$, que considera vecino a todos los sectores que comparten un lado o una esquina con un SU; y una matriz de distancia inversas entre los centroides de los SU, restringiendo la vecindad a aquellos centroides que están a menos de 1 km ($W_d$). El valor de un kilómetro es arbitrario, aunque razonable en la escala humana. Los grafos que representan las 2 matrices $W$ se muestran en la figura 4.9.

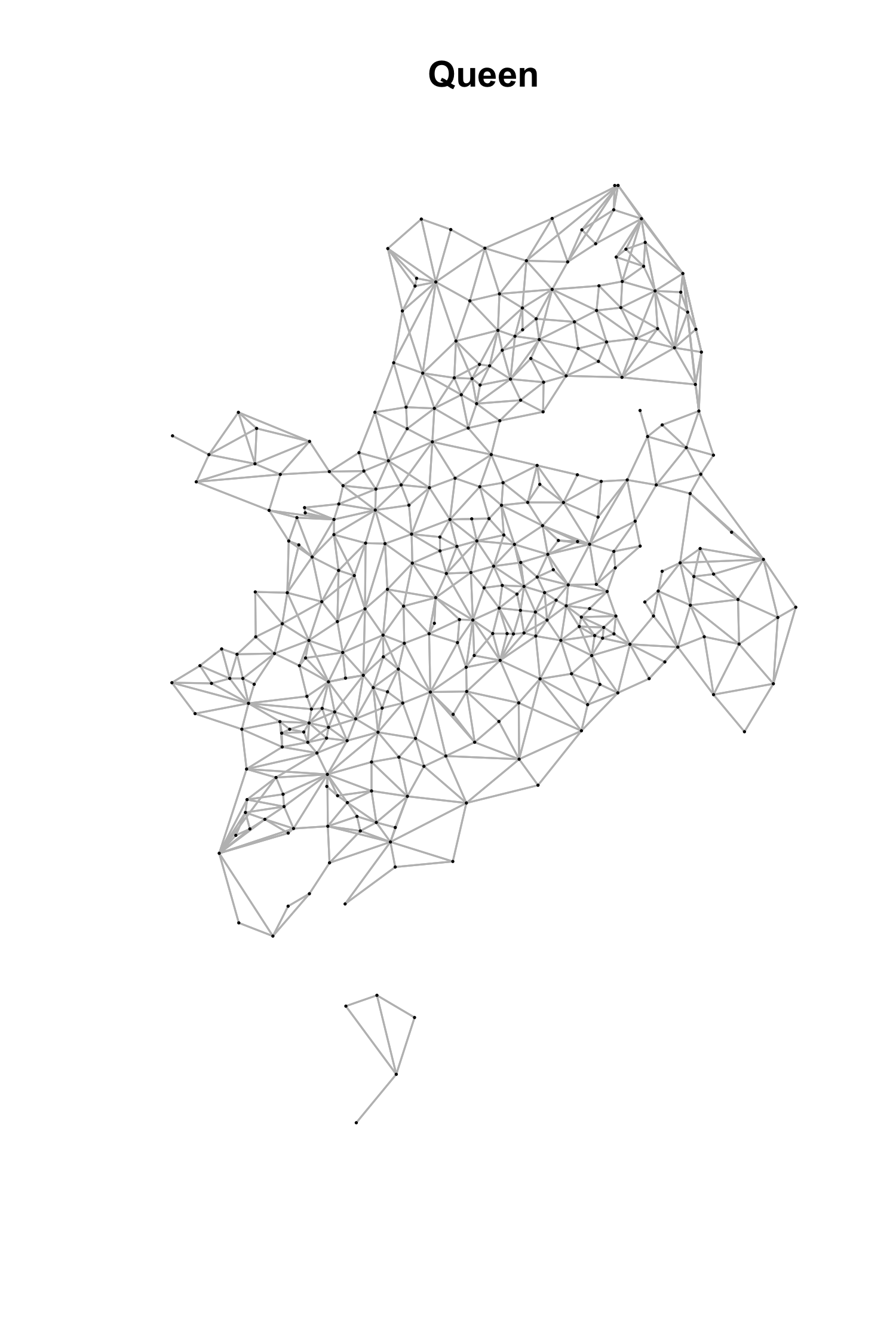
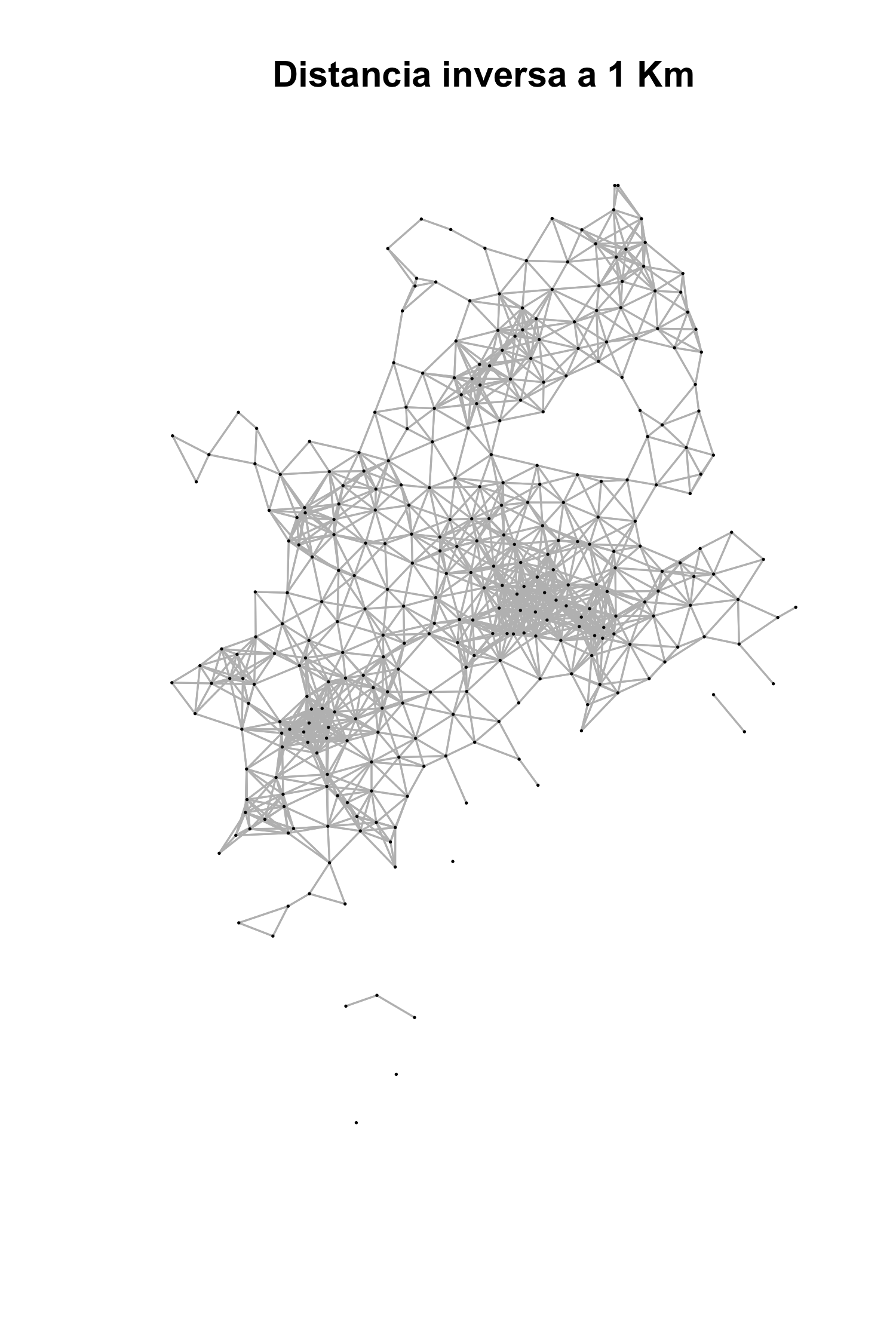
Figura 4.9: Matrices de vecindad del análisis espacial

4.1.3.1 Autocorrelación variables dependientes

Se analizó la autocorrelación de las variables dependientes para encontrar agrupaciones existentes en los datos que pueden ser explicados por la estructura de vecindad. Los resultados de los test de Moran’I para ambas variables dependientes muestran que existen patrones de agrupamiento y que puede rechazarse la hipótesis nula de que los procesos espaciales subyacentes son aleatorios (ver tablas 4.4 y 4.5).

Ambos diseños de matriz revelan presencia clara de autocorrelación espacial. La matriz $W_q$ captura mejor la autocorrelación del área de copa. En el caso de la cobertura de copa la matriz $W_d$ presenta un valor ligeramente mayor de autocorrelación.

Los mapas LISA muestran los grupos de sectores que configuran la autocorrelación del área de copa usando la matriz para $W_q$ (figura 4.10) y los grupos de la variable cobertura de copa usando la matriz $W_d$ (figura 4.13).

Los grupos que se forman muestran patrones distintos en los dos indicadores seleccionados para caracterizar los beneficios del arbolado urbano. Sin embargo, existen SU comunes en los grupos conformados pero con diferencias en la extensión de los conglomerados identificados. Esto se debe a que cada uno de los indicadores expresa un concepto distinto del disfrute de ese beneficio: el área de copa muestra las diferencias desde una perspectiva global, es decir, con base en el valor absoluto de área de copa de un SU en relación al total de área disponible en toda la ciudad. El indicador de cobertura de copa expresa el beneficio de forma relativa entre los SU al dividir el área de copa disponible en un SU entre el área pública de ese SU.

Es clara la similitud entre los grupos obtenidos para una misma variable dependiente con ambos diseños de matriz $W$ (figura 4.10 y figura 4.11 para el área de copa y 4.12 y 4.13 para la cobertura de copa), posiblemente porque no existen diferencias notables entre los dos tipos de estructura de vecindad propuestas (figura 4.9).

Tabla 4.4: Test de Moran - Área de copa para $W_q$ y $W_d$
	$W_q$	$W_d$
Estadístico Moran I	0.37488	0.28174
Expectativa	-0.00310	-0.00312
Varianza	0.00119	0.00090
Desviación estándar de Moran I	10.95802	9.50984
p-valor	0.00000	0.00000

Tabla 4.5: Test de Moran - Porcentaje de cobertura de copa para $W_q$ y $W_d$
	$W_q$	$W_d$
Estadístico Moran I	0.48104	0.50225
Expectativa	-0.00310	-0.00312
Varianza	0.00118	0.00089
Desviación estándar de Moran I	14.10670	16.95747
p-valor	0.00000	0.00000

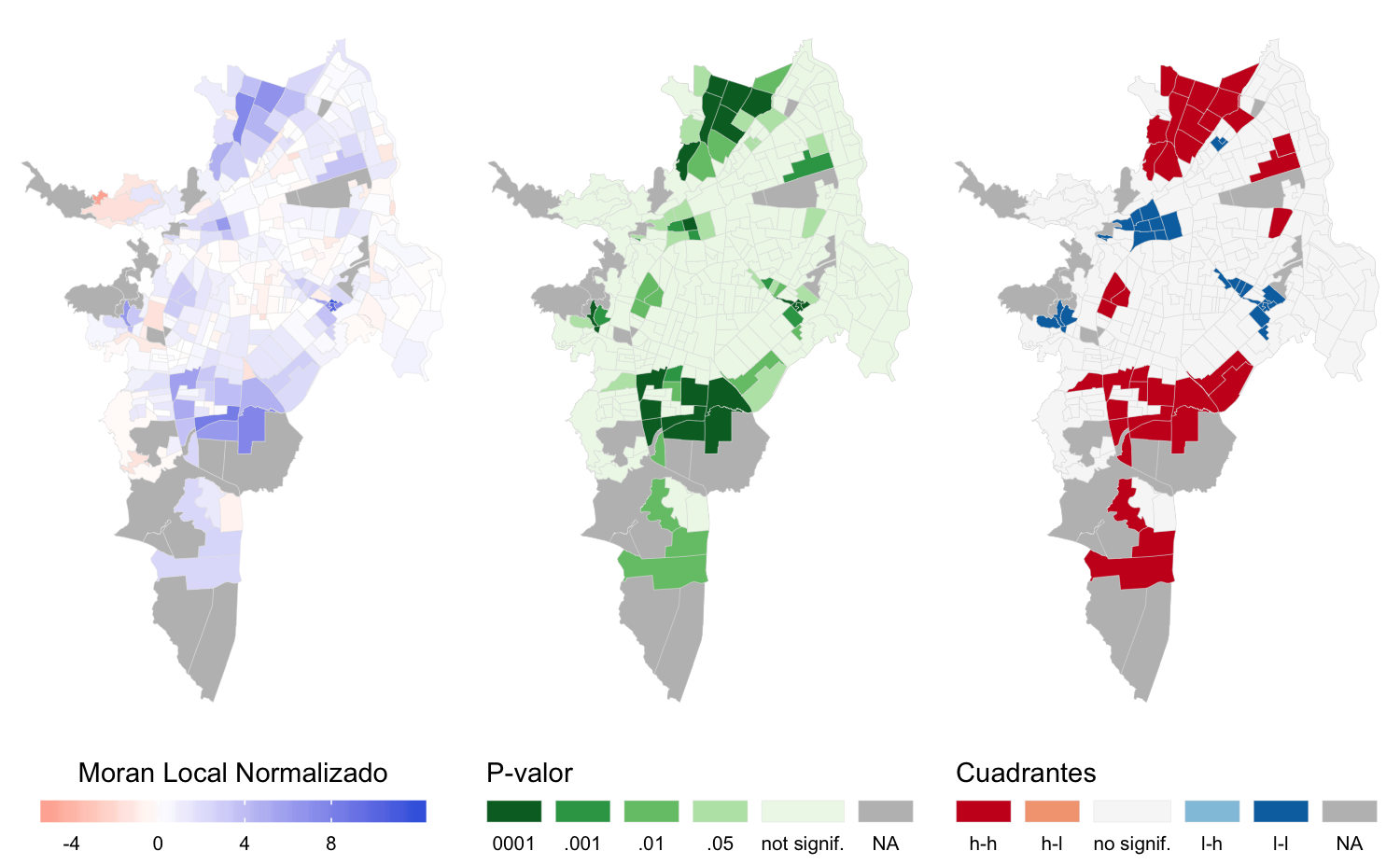
Figura 4.10: Mapas LISA para la matriz $W_q$ del indicador área de copa

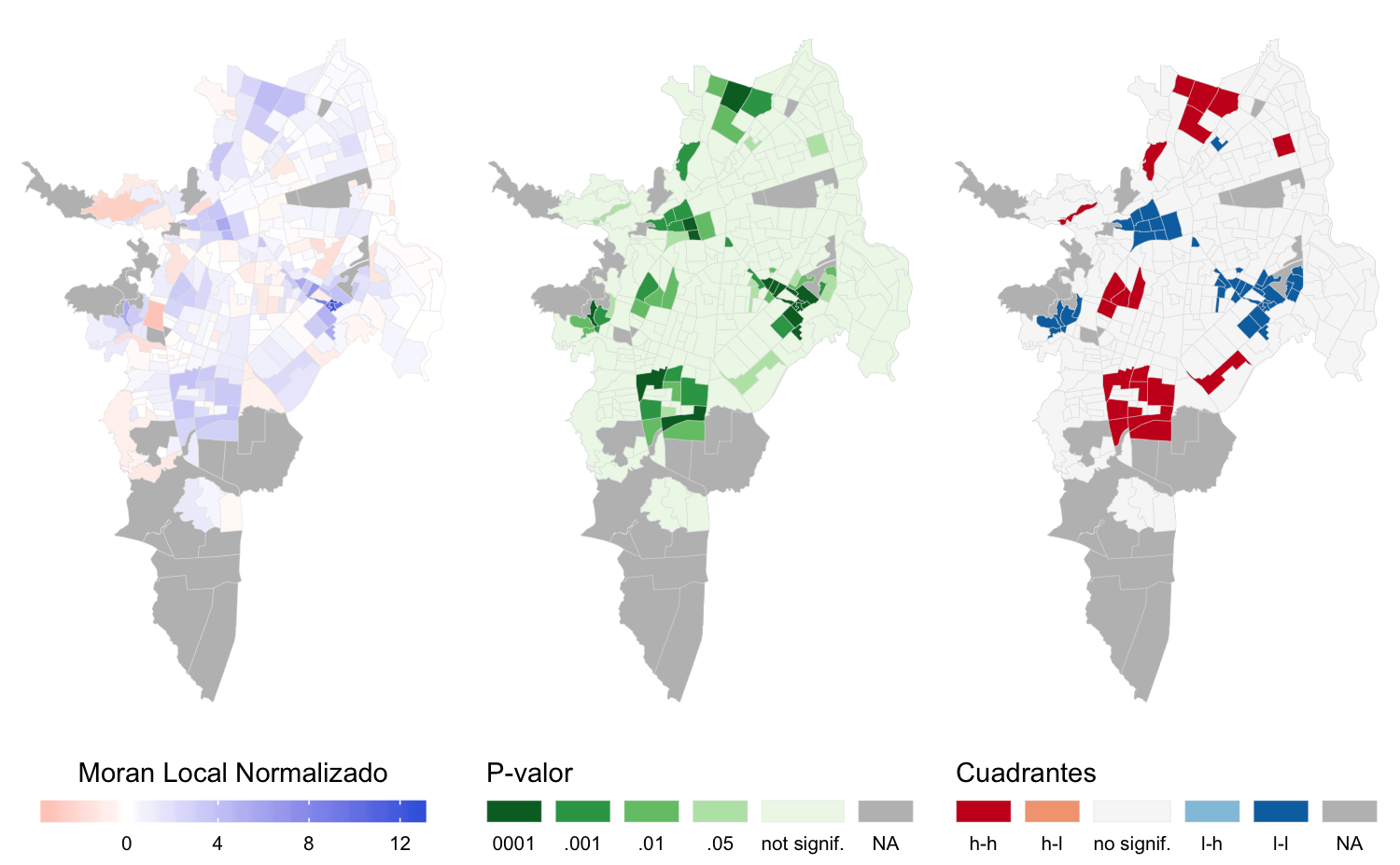
Figura 4.11: Mapas LISA para la matriz $W_d$ del indicador área de copa

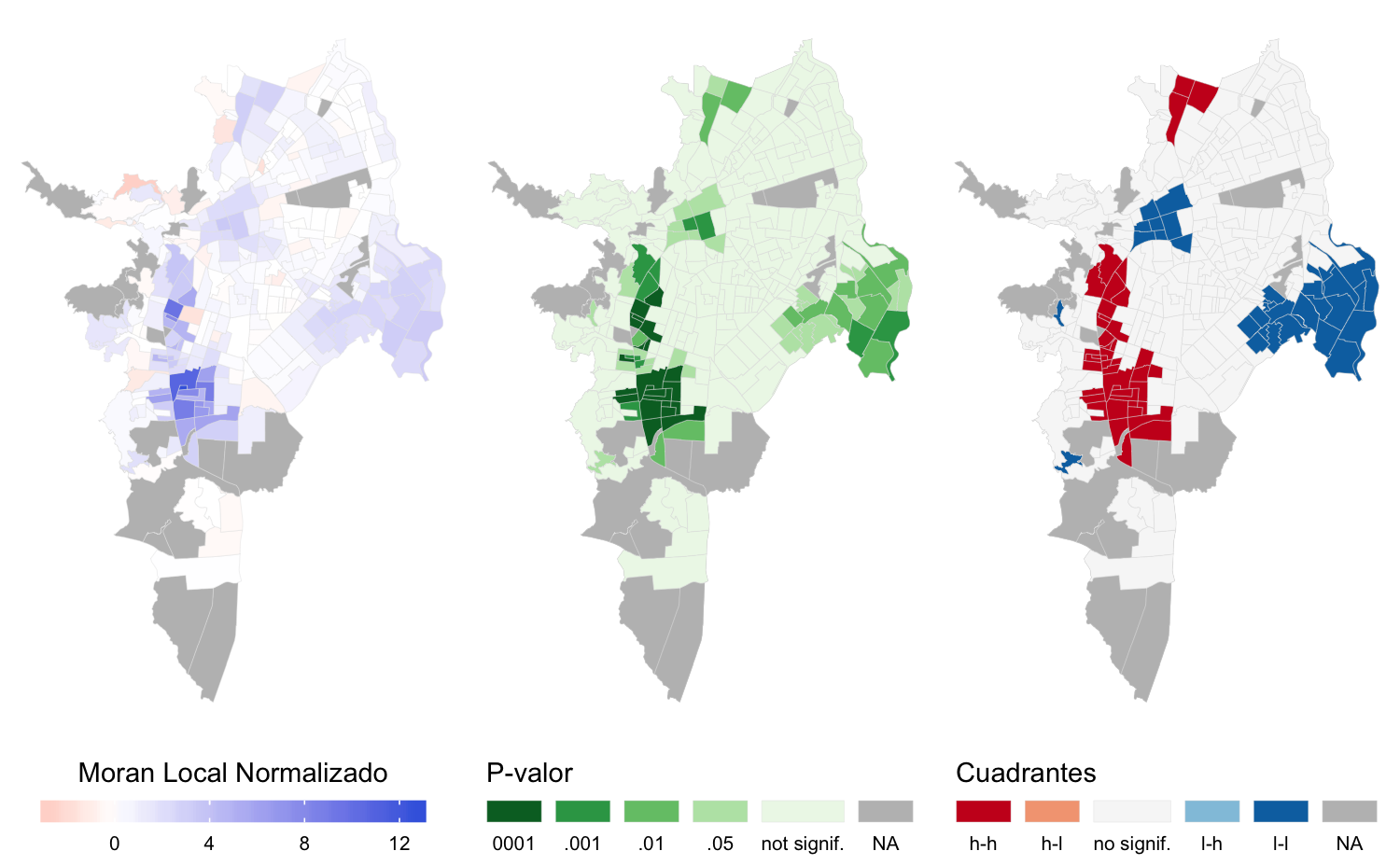
Figura 4.12: Mapas LISA para la matriz $W_q$ del indicador cobertura de copa

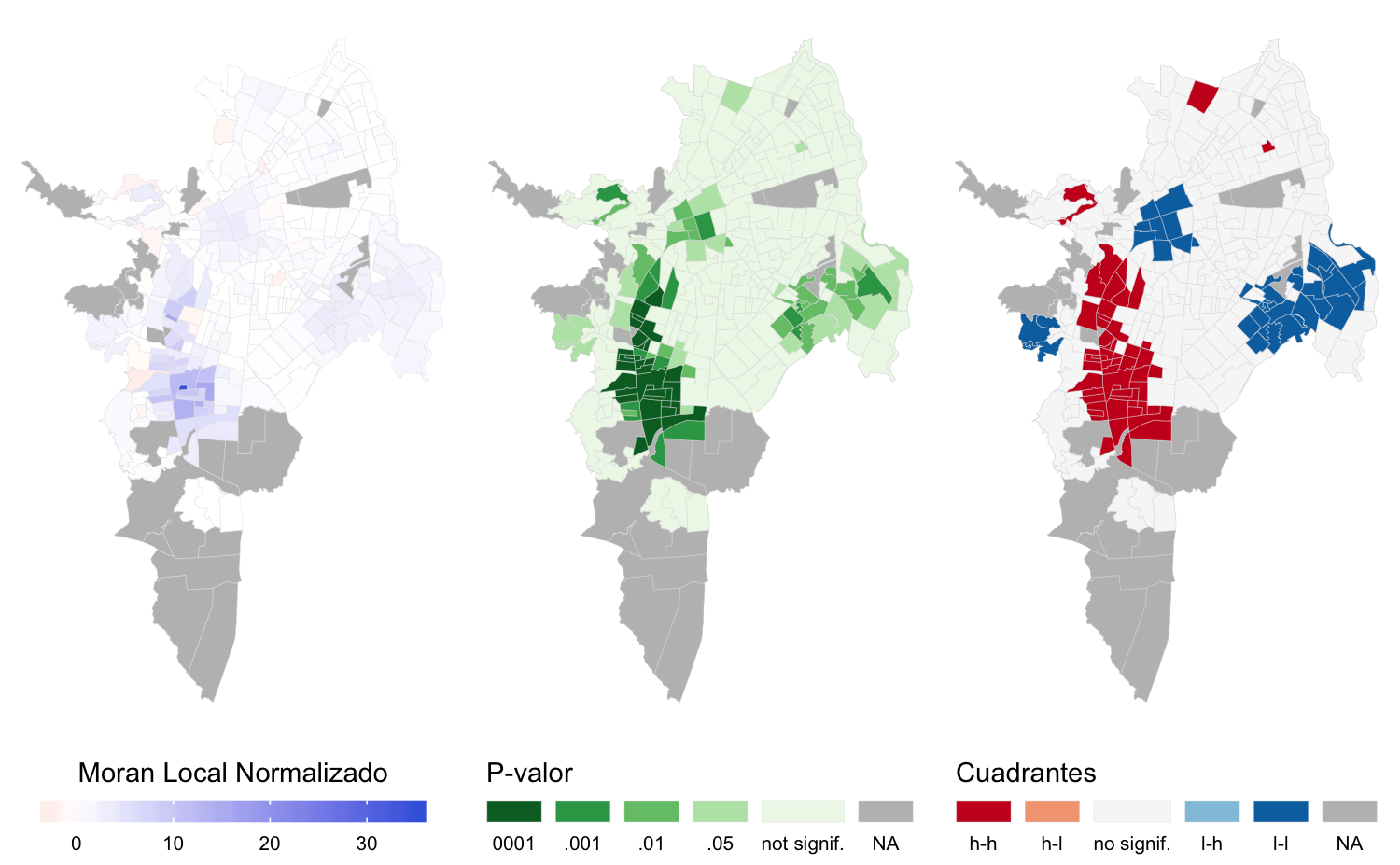
Figura 4.13: Mapas LISA para la matriz $W_d$ de del indicador cobertura de copa

4.1.3.2 Autocorrelación residuos de los OLS

Para evaluar la utilidad de aplicar modelos espaciales de regresión se examinó la existencia de autocorrelación en los residuos de los modelos de regresión lineal. Se comparó si alguno de las estructuras de vecindad produce resultados significativamente mejores en la detección de autocorrelación espacial.

La tabla 4.6 muestra ambos diseños de matriz $W$ presentan un valor de Moran Global mayor que 0 y significativo para los residuos del OLS de área de copa, al igual que para los residuos del OLS del porcentaje de cobertura (ver tabla 4.7).

En ambos modelos el resultado de autocorrelación espacial sugiere que al introducir retardos espaciales y la estructura de vecindad pueden mejorar la estimación de los coeficientes de la regresión y las métricas de desempeño del ajuste.

Tabla 4.6: Test de Moran - Residuos de OLS Área de copa para $W_q$ y $W_d$
	$W_q$	$W_d$
Estadístico Moran I	0.09660	0.11579
Expectativa	-0.00310	-0.00312
Varianza	0.00119	0.00090
Desviación estándar de Moran I	2.89161	3.97182
p-valor	0.00192	0.00004

Tabla 4.7: Test de Moran - Residuos de OLS Porcentaje de cobertura de copa para $W_q$ y $W_d$
	$W_q$	$W_d$
Estadístico Moran I	0.19436	0.18821
Expectativa	-0.00310	-0.00312
Varianza	0.00117	0.00088
Desviación estándar de Moran I	5.78107	6.45120
p-valor	0.00000	0.00000

4.1.3.3 Modelo espacial área de copa

Las métricas de ajuste de los modelos con las matrices de vecindad $W_d$ (ver tabla 4.9) y $W_q$ (tabla 4.8) para el área de copa muestran que los modelos espaciales logran eliminar la autocorrelación espacial global en los residuos. Es importante anotar que la heterocedasticidad reportada en la tabla 4.3 del modelo OLS desaparece al descartar las variables independientes con $p$-valores no significativos, por lo que no se le puede adjudicar al uso de los términos espaciales. Todos los modelos mejoran las métricas de error respecto del OLS y ninguno logra la normalidad en los residuos, aunque en las gráficas diagnósticas se aprecia una semblanza aceptable (ver figura 4.14) con problemas en valores extremos.

Al comparar los resultados usando el desempeño en criterio de información de Akaike (AIC), el mejor fue el SEM con la matriz $W_d$, seguido del SD con $W_q$, con leves diferencias entre las métricas. En cuanto a $\lambda$ (tabla 4.11) y $\rho$ (tabla 4.13) , los términos autorregresivos, son significativos para SEM $W_d$ y para SD con $W_q$ respectivamente.

El resultado del modelo SEM confirma la significancia de las variables de cantidad de personas con estudios superiores y porcentaje de espacio verde, con coeficientes de valores positivos, en ese orden de importancia. La densidad de población y la presencia de viviendas tipo cuarto, con coeficientes negativos, son factores que disminuyen la disponibilidad de área de copa en un SU (ver tabla 4.10). Existen cambios y ajustes en los valores de los coeficientes con relación al modelo OLS, que dadas las mejoras en las métricas de ajuste hacen más confiables las estimaciones.

Tabla 4.8: Metricas de ajuste para los modelos de área de copa $W_q$
medidasfit	OLS	SAR	SEM	SD
Globla Moran’I	0.09660	-0.01056	-0.01056	-0.00157
GMI p-value	0.00192	0.58578	0.58574	0.48239
Shapiro-Wilk	0.97939	0.97959	0.97638	0.98307
SW p-value	0.00013	0.00015	0.00004	0.00073
Breusch-Pagan	6.70653	4.36429	5.08935	10.28094
BP p-value	0.15223	0.35894	0.27825	0.24586
Media Residuos	0.00000	0.00000	0.00000	0.00000
MSE	0.00345	0.00330	0.00335	0.00322
adj-Rsquare	0.60639	NA	NA	NA
Nagelkerke pseudo-R-squared	NA	0.62529	0.61948	0.63462
AIC	-905.09560	-914.99865	-910.01741	-915.17149
Log likelihood	458.54780	464.49933	462.00870	468.58574

Tabla 4.9: Metricas de ajuste para los modelos de área de copa con $W_d$
medidasfit	OLS	SAR	SEM	SD
Globla Moran’I	0.11579	0.08293	-0.01362	0.07133
GMI p-value	0.00004	0.00202	0.63708	0.00645
Shapiro-Wilk	0.97939	0.98468	0.97628	0.98522
SW p-value	0.00013	0.00160	0.00003	0.00210
Breusch-Pagan	6.70653	8.80615	5.51317	11.99026
BP p-value	0.15223	0.06613	0.23857	0.15164
Media Residuos	0.00000	0.00000	-0.00001	0.00000
MSE	0.00345	0.00340	0.00327	0.00333
adj-Rsquare	0.60639	NA	NA	NA
Nagelkerke pseudo-R-squared	NA	0.61640	0.62586	0.62438
AIC	-905.09560	-907.40643	-915.49806	-906.21535
Log likelihood	458.54780	460.70321	464.74903	464.10768

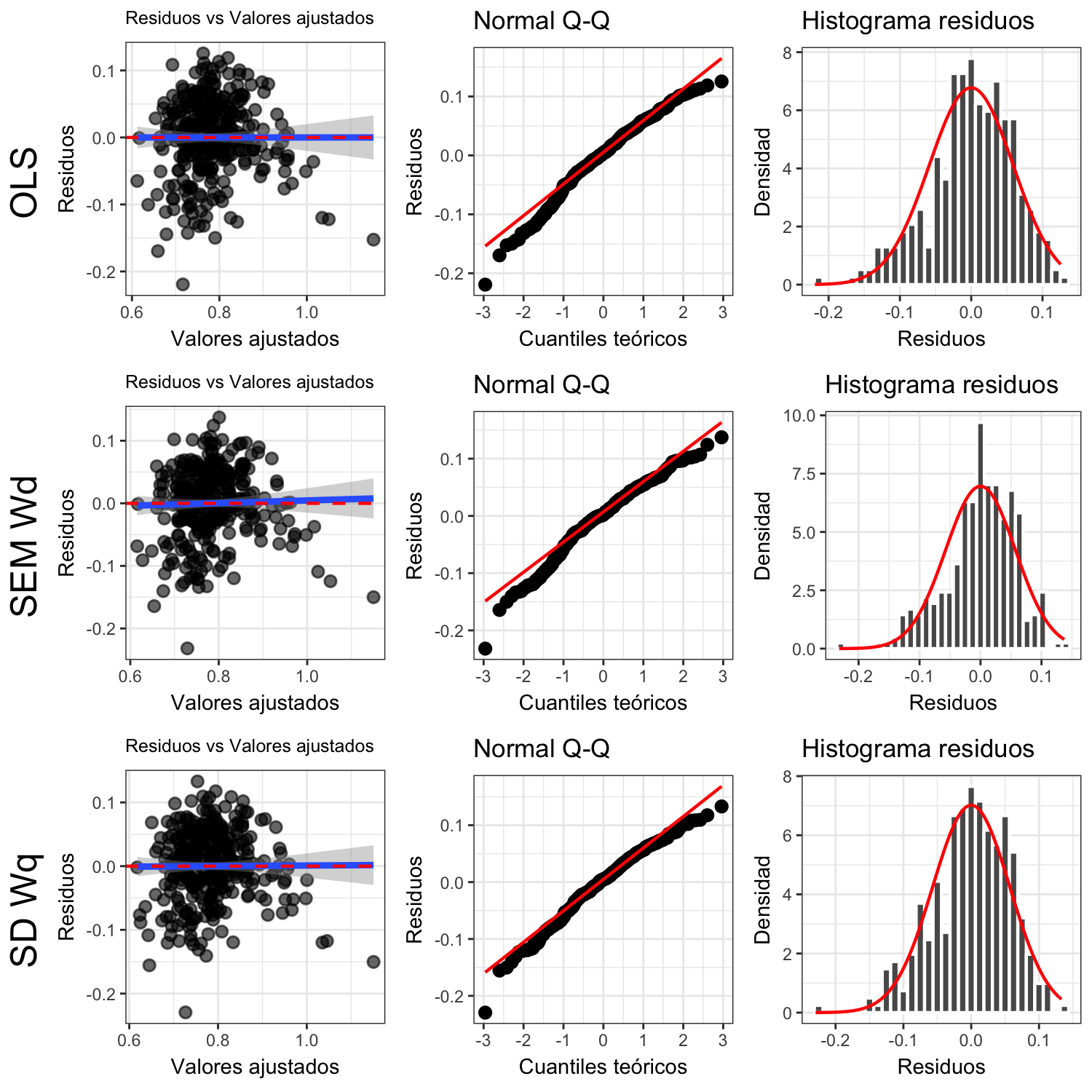
Figura 4.14: Diagnóstico comparativo entre modelos espaciales de área de copa

Tabla 4.10: Coeficientes del modelo SEM de área de copa $W_d$
Término	Estimado	Error std.	t-valor
Intercepto	0.779	0.009	83.105
con estudios superiores	0.299	0.023	13.154
densidad de población	-0.140	0.019	-7.359
vivienda tipo cuarto [%]	-0.132	0.032	-4.168
área de EV	0.133	0.027	4.871

Tabla 4.11: Coeficiente de autocorrelación modelo SEM de área de copa $W_d$
$\lambda$	Likelihood ratio	p-valor
0.316	12.402	0

Tabla 4.12: Coeficientes del modelo SD de área de copa $W_q$
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	0.637	0.065	9.828	0.000
con estudios superiores	0.287	0.024	12.023	0.000
densidad de población	-0.096	0.025	-3.783	0.000
vivienda tipo cuarto [%]	-0.059	0.041	-1.438	0.151
área de EV	0.141	0.030	4.689	0.000
estudios superiores (retardada)	-0.016	0.047	-0.331	0.741
densidad de población (retardada)	-0.050	0.037	-1.356	0.175
vivienda tipo cuarto [%] (retardada)	-0.146	0.065	-2.226	0.026
área de EV (retardada)	-0.074	0.040	-1.832	0.067

Tabla 4.13: Coeficiente de autocorrelación modelo SD de área de copa $W_q$
$\rho$	Likelihood ratio	p-valor
0.201	6.415	0.011

4.1.3.4 Modelo espacial porcentaje de cobertura de área de copa

Las métricas de ajuste de los modelos con las matrices de vecindad $W_d$ (ver tabla 4.15) y $W_q$ (tabla 4.14) para el porcentaje de cobertura de copa muestran que los modelos espaciales logran eliminar la autocorrelación espacial global en los residuos, excepto el SAR con $W_d$. Todos los modelos mejoran las métricas de error con respecto al OLS y ninguno logra la normalidad en los residuos ni eliminar la heterocedasticidad como se aprecia en las gráficas diagnósticas (ver figura 4.15).

Al comparar los resultados usando el desempeño en AIC, el mejor fue el SD con la matriz $W_d$. $\rho$, el término autorregresivo, es de un valor alto y muy significativo para el modelo SD con $W_d$ (tabla 4.16).

El resultado del modelo SD confirma la significancia de la única variable independiente: porcentaje de personas con estudios superiores, con coeficiente positivo, identificándolo como un factores relacionado con alta proporción de área de copa en un SU (ver tabla 4.17). Existen una reducción del valor del coeficiente con relación al modelo OLS.

La variable de estudios superiores en la población refleja el patrón de agrupamiento espacial de la cobertura de copa pero es poco significativa como variable retardada, cuestión que pone dudas sobre si el SD proponga una interpretación acertada o diferente de un modelo autorregresivo puro (SAR).

Tabla 4.14: Metricas de ajuste para los modelos de porcentaje de área de copa $W_q$
medidasfit	OLS	SAR	SEM	SD
Globla Moran’I	0.19436	0.00734	-0.01131	-0.00863
GMI p-value	0.00000	0.37996	0.59509	0.56441
Shapiro-Wilk	0.90492	0.89936	0.89238	0.89685
SW p-value	0.00000	0.00000	0.00000	0.00000
Breusch-Pagan	16.82734	16.22458	15.21537	17.19946
BP p-value	0.00004	0.00006	0.00010	0.00018
Media Residuos	0.00000	0.00000	0.00000	0.00000
MSE	0.01100	0.00979	0.00981	0.00972
adj-Rsquare	0.45512	NA	NA	NA
Nagelkerke pseudo-R-squared	NA	0.50267	0.49988	0.50390
AIC	-535.66434	-562.24323	-560.43438	-561.04776
Log likelihood	270.83217	285.12162	284.21719	285.52388

Tabla 4.15: Metricas de ajuste para los modelos de porcentaje de área de copa $W_d$
medidasfit	OLS	SAR	SEM	SD
Globla Moran’I	0.18821	0.07353	0.00335	0.01940
GMI p-value	0.00000	0.00487	0.41351	0.22373
Shapiro-Wilk	0.90492	0.89936	0.88316	0.90138
SW p-value	0.00000	0.00000	0.00000	0.00000
Breusch-Pagan	16.82734	16.22458	10.35903	17.66672
BP p-value	0.00004	0.00006	0.00129	0.00015
Media Residuos	0.00000	0.00000	0.00017	0.00000
MSE	0.01100	0.00979	0.00950	0.00931
adj-Rsquare	0.45512	NA	NA	NA
Nagelkerke pseudo-R-squared	NA	0.50267	0.51018	0.52395
AIC	-535.66434	-562.24323	-567.17585	-574.41489
Log likelihood	270.83217	285.12162	287.58793	292.20744

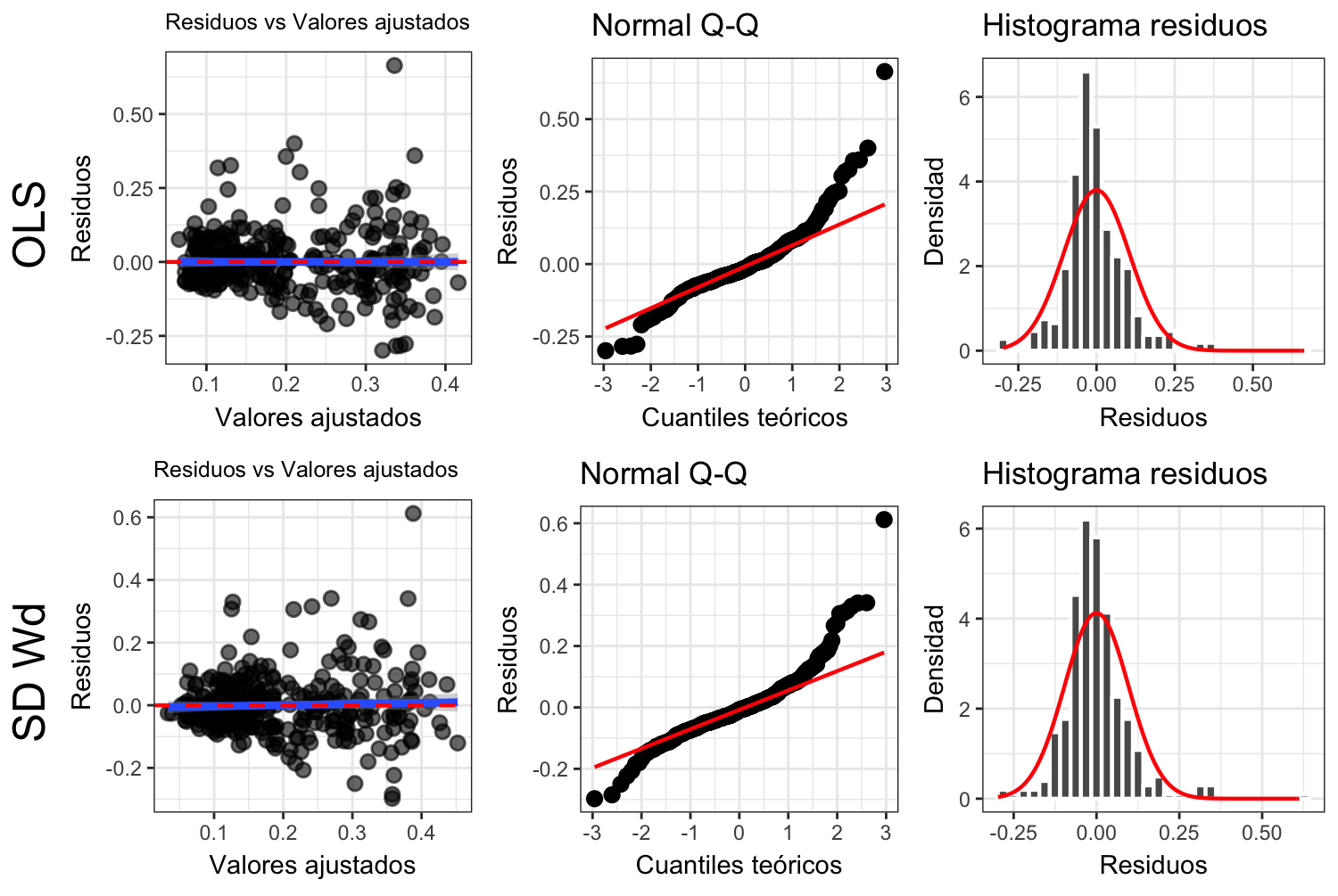
Figura 4.15: Diagnóstico comparativo entre modelos de porcentaje de copa

Tabla 4.16: Coeficiente de autocorrelación modelo SD $W_d$ de porcentaje de área de copa
$\rho$	Likelihood ratio	p-valor
0.465	32.069	0

Tabla 4.17: Coeficientes del modelo SD de porcentaje de área de copa $W_d$
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	0.023	0.011	2.206	0.027
con estudios superiores [%]	0.239	0.034	6.941	0.000
estudios superiores [%] (retardada)	-0.021	0.050	-0.407	0.684

4.2 Acceso a espacios verdes

En el caso de los EV la literatura ofrece variedad de medidas sobre acceso en relación con la distancia o con el área disponible. Se eligieron dos métricas: el porcentaje de área de espacio verde de un sector censal, para cuantificar beneficios a nivel local; y la razón área disponible entre distancia (ia.areas.dist) (ecuación (3.2)) que expresa el acceso más allá de los límites del SU. El valor es cercano a cero cuando el área disponible es cercana a cero o cuando la distancia es mucho mayor que el área media de espacio verde en el radio de búsqueda, limitado a 1000 $m$, un orden de magnitud menor que el área media de EV (22,971.4 $m^2$). La distancia promedio del centroide de un SU al conjunto de EV es 644.7 $m$. Como se observa en la figura 4.16, esta medición parece un versión interpolada del indicador local de acceso porcentaje de área de EV (area_ep.porcentaje), y hace evidente un patrón espacial de grupos con mejor acceso a EV, no uniforme ni aleatorio.

Al examinar la distribución de los valores de estos indicadores (figuras 4.17 y 4.18) se observa que en ambos indicadores existe asimetría positiva, lo que muestra una concentración de valores por debajo del promedio del indicador y un conjunto reducido de SU muy por encima.

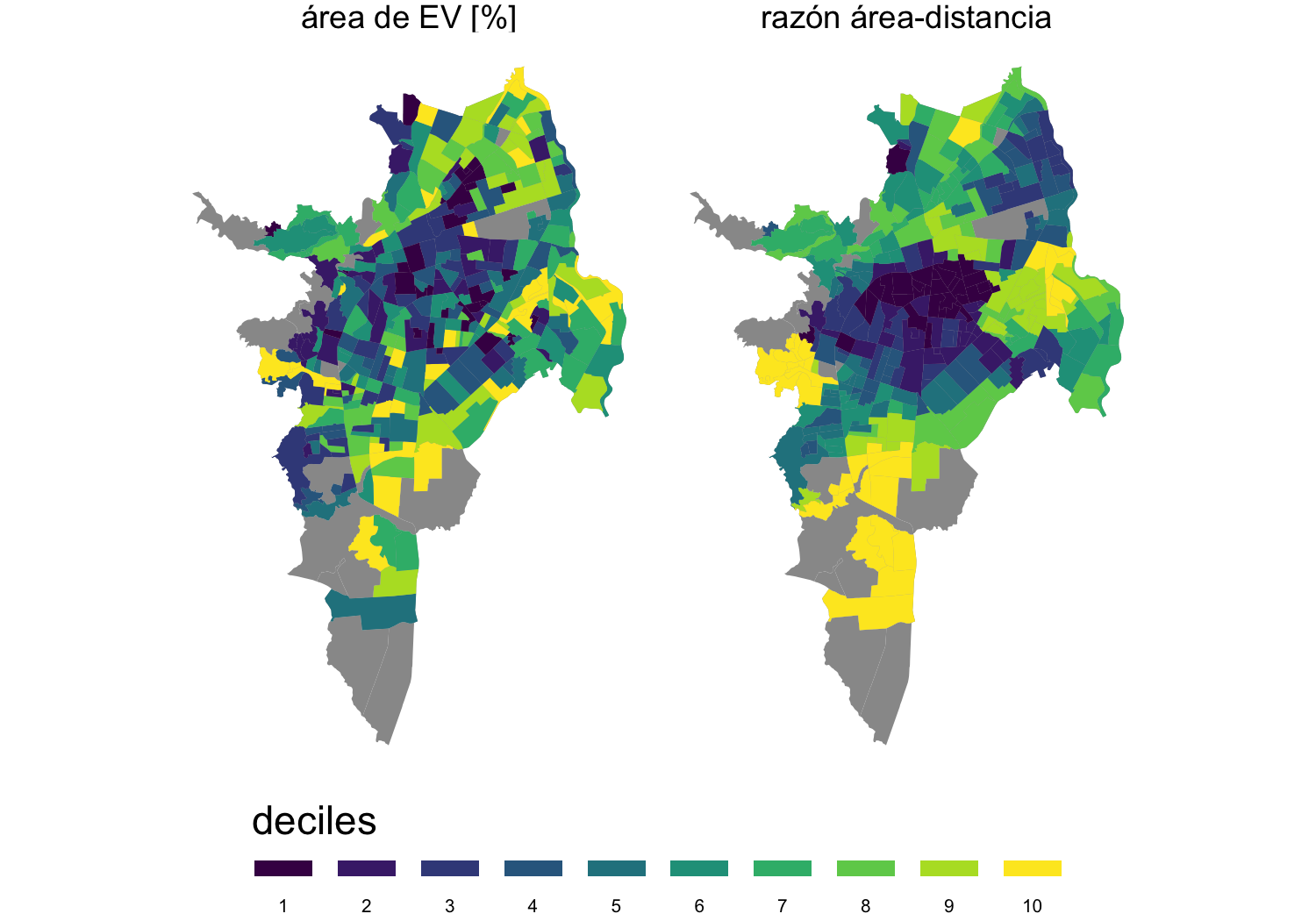
Figura 4.16: Métricas de acceso a espacio verdes seleccionadas

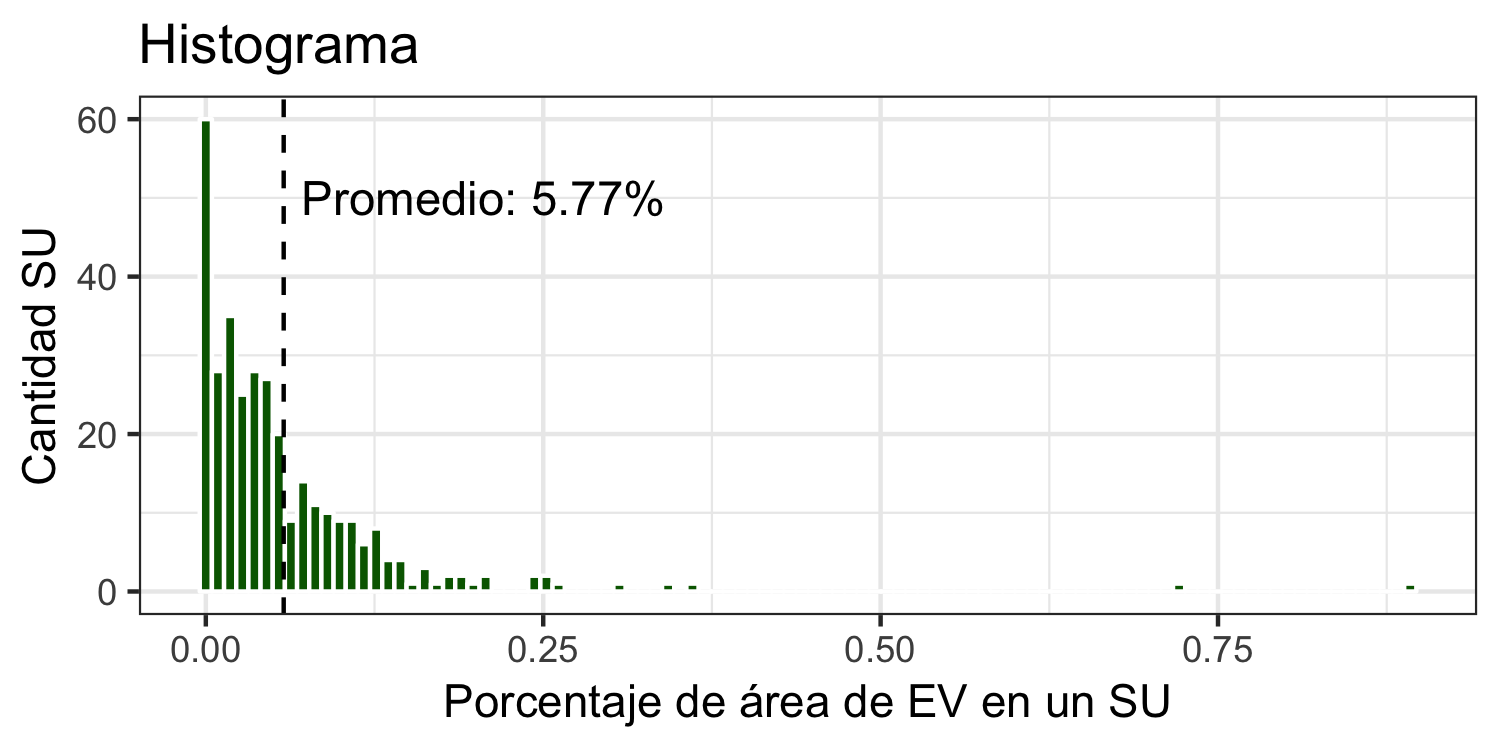
Figura 4.17: Distribucion del indicador de acceso local a EV

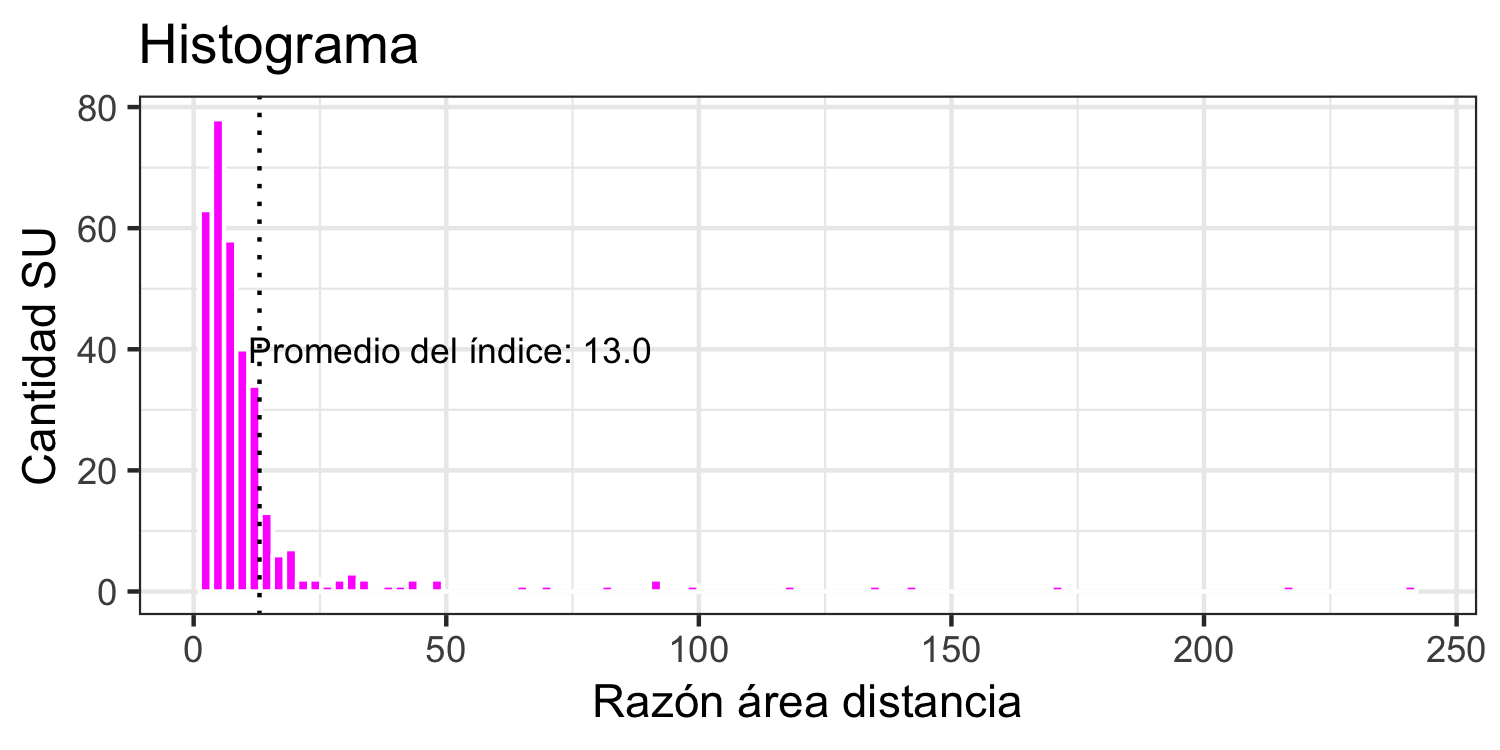
Figura 4.18: Distribucion del indicador de acceso a EV área-distancia

4.2.1 Correlaciones y distribuciones bivariadas

Las figuras 4.19 y 4.20 resumen los resultados del cálculo de los coeficientes de Pearson y Spearman respectivamente de las variables poblacionales y los indicadores de acceso. Esta relación es muy débil, y en todas las variables (y para ambos coeficientes de correlación) es inferior a 0.3, un valor considerado bajo para seleccionar una variable como candidata a predictor de una regresión lineal. Sin embargo, como parte del proceso para indagar sobre el efecto en la estimación de parámetros de los modelos geoestadísticos, se incluyeron las de mejor correlación: densidad de población, con alguna limitación [%] para el índice de acceso razón área-distancia y ningún estudio [%] para área de EV [%].

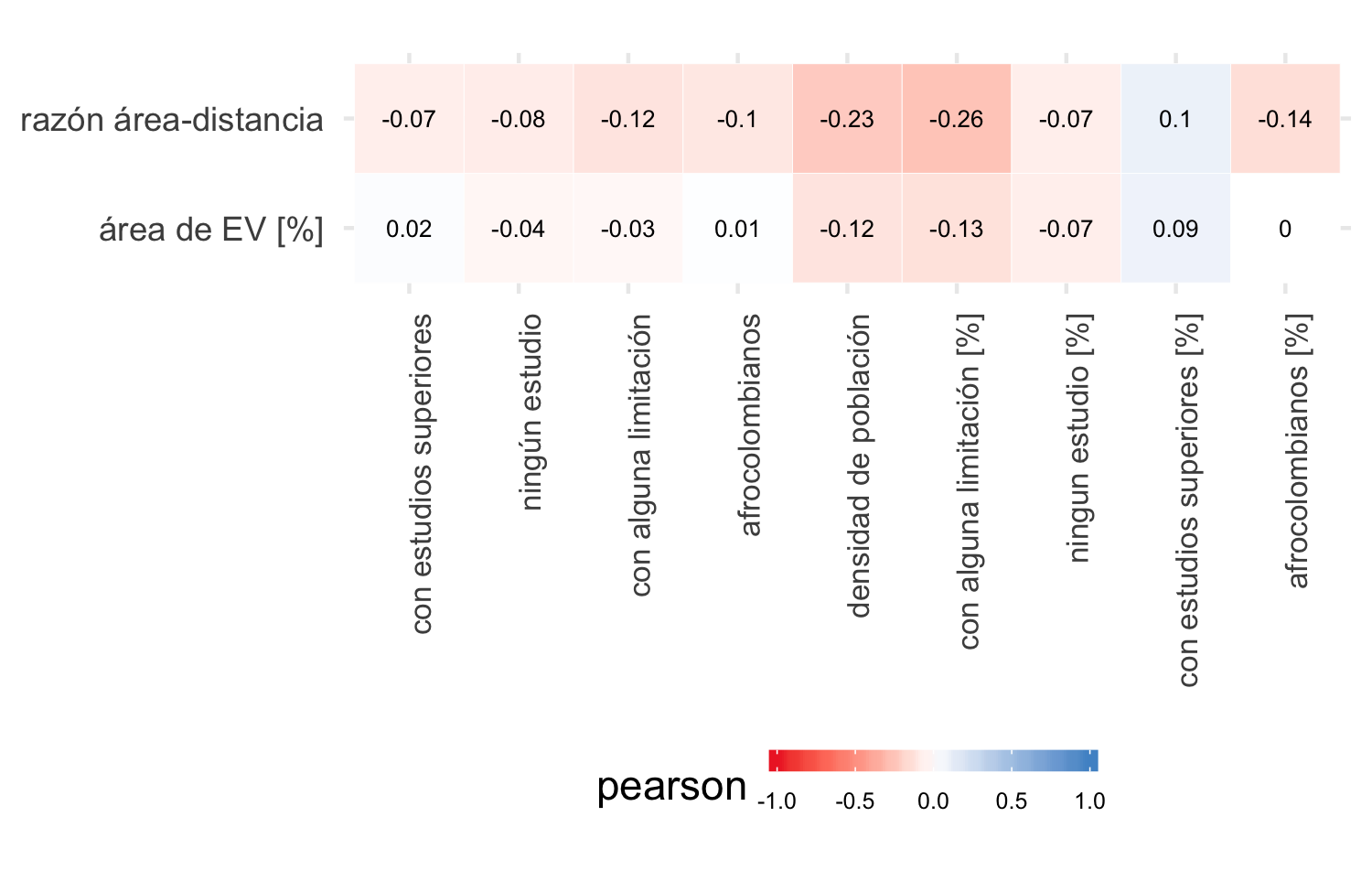
Figura 4.19: Coeficiente Pearson entre acceso a EV y variables de población

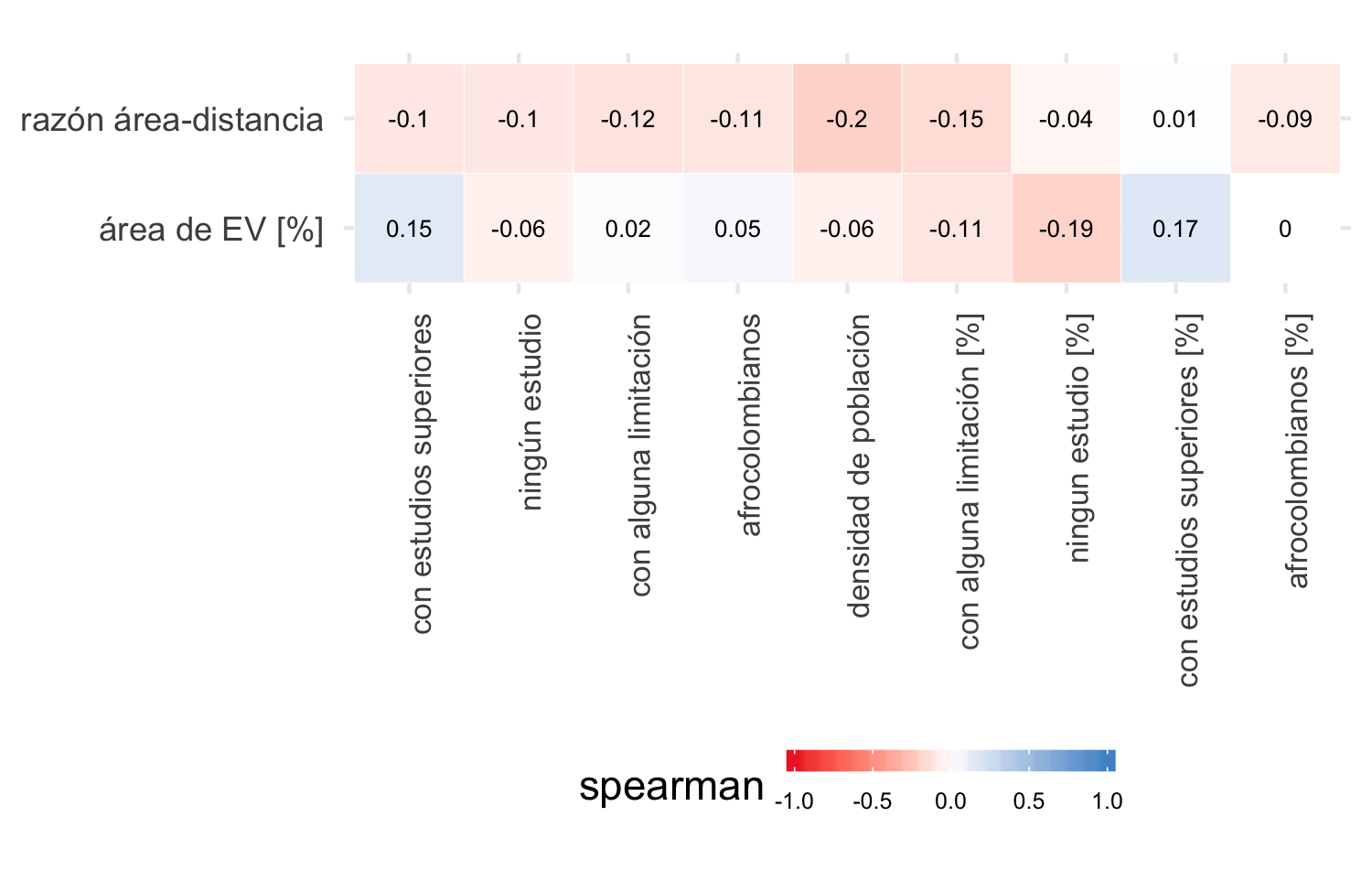
Figura 4.20: Coeficiente Spearman entre acceso a EV y variables de población

El conjunto de variables sobre el uso de los predios y sus coeficientes de correlación con las variables dependientes se muestran en las figuras 4.21 y 4.22. De nuevo las correlaciones son bajas, y aparentemente poco explicativas de los índices de acceso. Las variables de uso de los predios que mejor se relacionan con los índices son: uso de unidad económica [%] y el viviendas tipo cuarto [%].

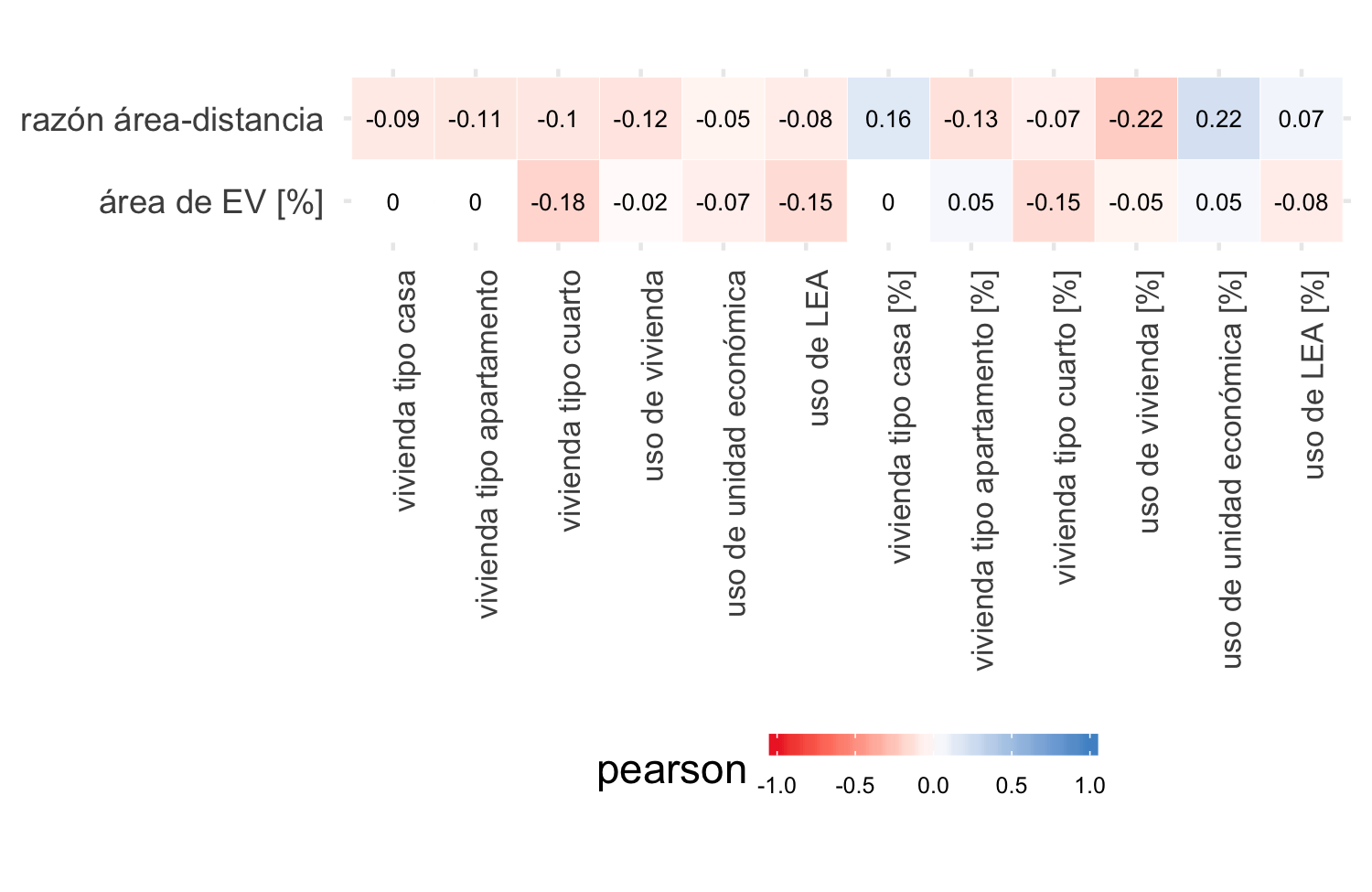
Figura 4.21: Coeficiente Pearson entre acceso a EV y variables de uso de los predios

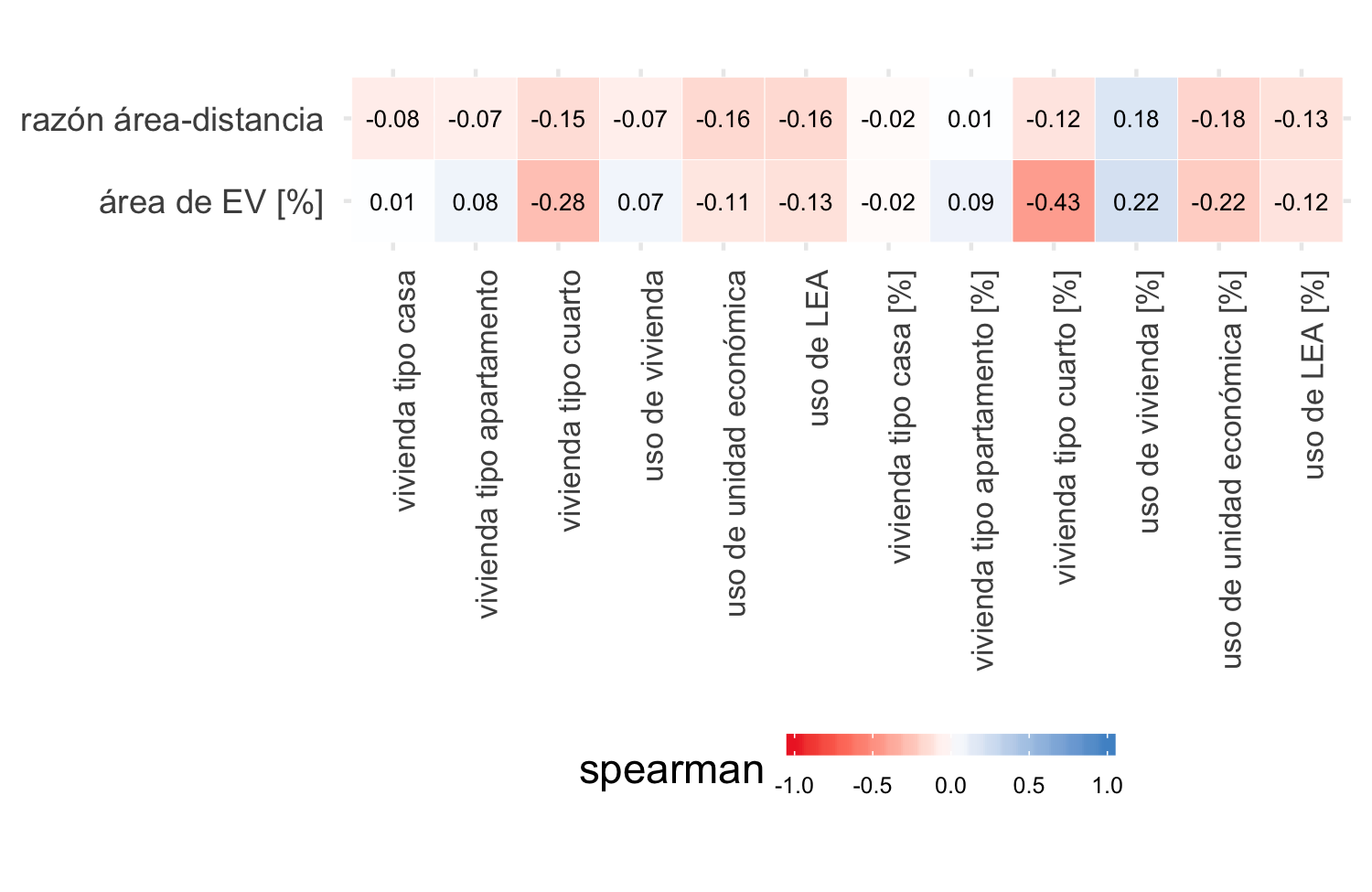
Figura 4.22: Coeficiente Spearman entre acceso a EV y variables de uso de los predios

El último bloque de variables indaga sobre las áreas y proporciones de las manzanas de cada sector censal y la vocación como pública o privada de los espacios dentro de un sector urbano. Las figuras 4.23 y 4.24 muestran que el área media de las manzanas (área media de manzana) de los sectores urbanos se relaciona de forma positiva con ambos índices de acceso, mucho más fuertemente que las variables poblacionales y de uso de predios. Aunque parece haber una fuerte correlación de los indicadores de acceso con las áreas privadas, públicas y del sector urbano, estas hacen parte de los cálculos que generan estos índices, produciendo en efecto ficticio en la correlación, razón por la que se incluyen en la modelación.

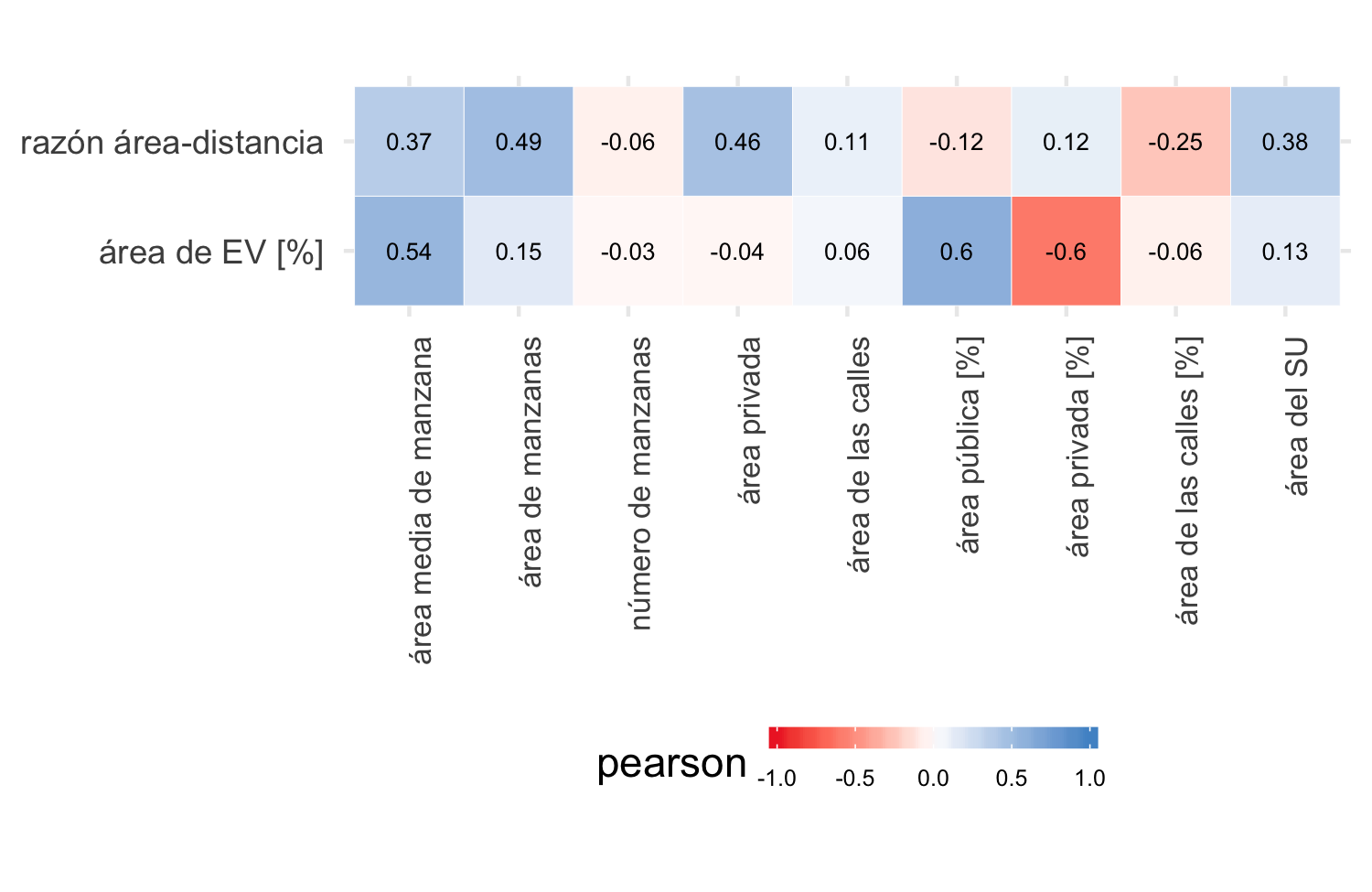
Figura 4.23: Coeficiente Pearson entre acceso a EV y variables sobre aspectos físicos de las manzanas y SU

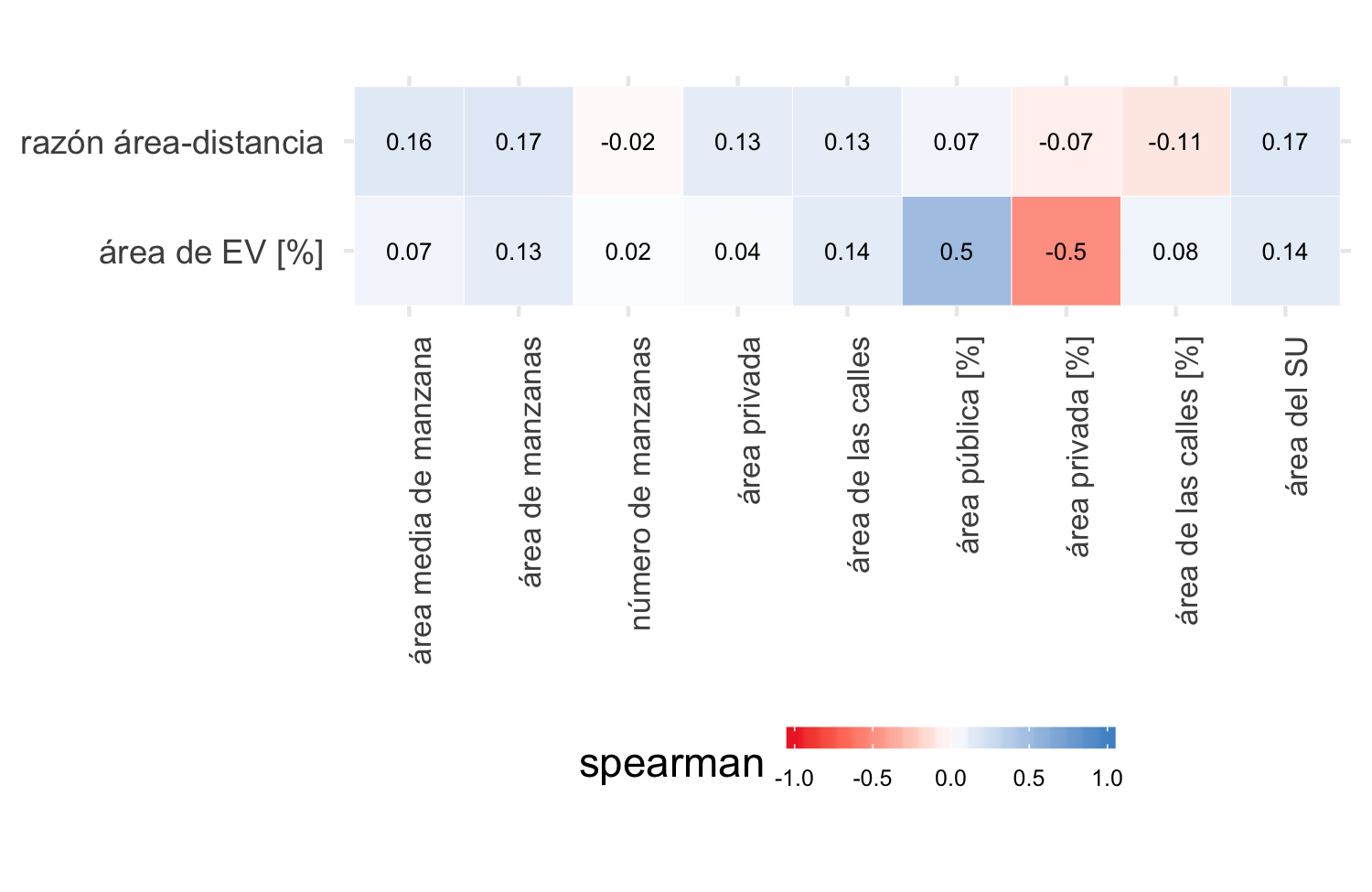
Figura 4.24: Coeficiente Spearman entre acceso a EV y variables sobre aspectos físicos de las manzanas y SU

En resumen, las variables independientes escogidas para los modelos lineales son:

Para el área de EV [%] los predictores seleccionados son ningun estudio [%], área media de manzana, vivienda tipo cuarto [%].
Para razón área-distancia los predictores seleccionados son densidad de población, con alguna limitación [%], uso de unidad económica [%], área media de manzana.

4.2.2 Modelos de regresión lineal EV

La tabla 4.18 muestra los coeficientes de la regresión para el porcentaje de EV; la tabla 4.19 muestra los coeficientes de la regresión para índice áreas-distancia, y la tabla 4.20 resume las métricas de ajuste de ambos modelos.

Los resultados de los test Shapiro-Wilk indican no normalidad en los residuos en ambos modelos, heterocedasticidad como muestra el test Breusch-Pagan y posibles no linealidades como se observa en las gráficas diagnósticas de la regresión de ambos modelos (ver figuras 4.25 y 4.26). El nivel explicativo de la variabilidad de los datos de ambos modelos es bajo. Sin embargo, el ajuste de ambos modelos tiene media de los residuos muy cercanas a 0, al igual que el error cuadrático medio (MSE).

Las variables significativas para el área de EV [%] son área media de manzana, vivienda tipo cuarto [%]. Estos resultados muestran que no existe evidencia significativa de que el acceso a EV en un SU esté relacionado con variables étnicas, de discapacidad o de acceso a la educación. Sin embargo es muy importante la relación positiva con aspectos estructurales representados por el área media de las manzanas y una relación negativa con el porcentaje de viviendas tipo cuarto, estas últimas concentradas en la zona centro y de ladera del área urbana de Santiago de Cali (ver figura 3.9).

Para la relación de área distancia se confirma la significancia de área media de manzana y, en ausencia de la variable vivienda tipo cuarto [%], se incorpora uso de unidad económica [%] que exhibe un patrón espacial similar. A diferencia del índice local de acceso, en razón área-distancia se evidenció una relación negativa con el porcentaje de personas con alguna limitación.

Para la siguientes fases se ignoraron las variables no significativas de los modelos lineales.

Tabla 4.18: Coeficientes OLS de Porcentaje de EV
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	0.03978	0.00826	4.81799	0.00000
ningun estudio [%]	0.05796	0.03665	1.58150	0.11474
área media de manzana	0.75792	0.06561	11.55207	0.00000
vivienda tipo cuarto [%]	-0.12801	0.04332	-2.95478	0.00336

Tabla 4.19: Coeficientes OLS de áreas-distancia
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	0.08879	0.02062	4.30576	0.00002
densidad de población	-0.02263	0.03137	-0.72126	0.47127
con alguna limitación [%]	-0.10709	0.03701	-2.89321	0.00407
uso de unidad económica [%]	0.08831	0.03838	2.30125	0.02201
área media de manzana	0.46186	0.08632	5.35076	0.00000

Tabla 4.20: Resumen métricas de ajuste OLS Indice contenedor (EV) y de acceso área-distancia
medidasfit	EV	Área-Distancia
Shapiro-Wilk	0.76782	0.55302
SW p-value	0.00000	0.00000
Breusch-Pagan	12.98572	51.60213
BP p-value	0.00151	0.00000
Media Residuos	0.00000	0.00000
MSE	0.00607	0.00923
adj-Rsquare	0.29656	0.17542
AIC	-737.84913	-597.63015
Log likelihood	372.92456	303.81507

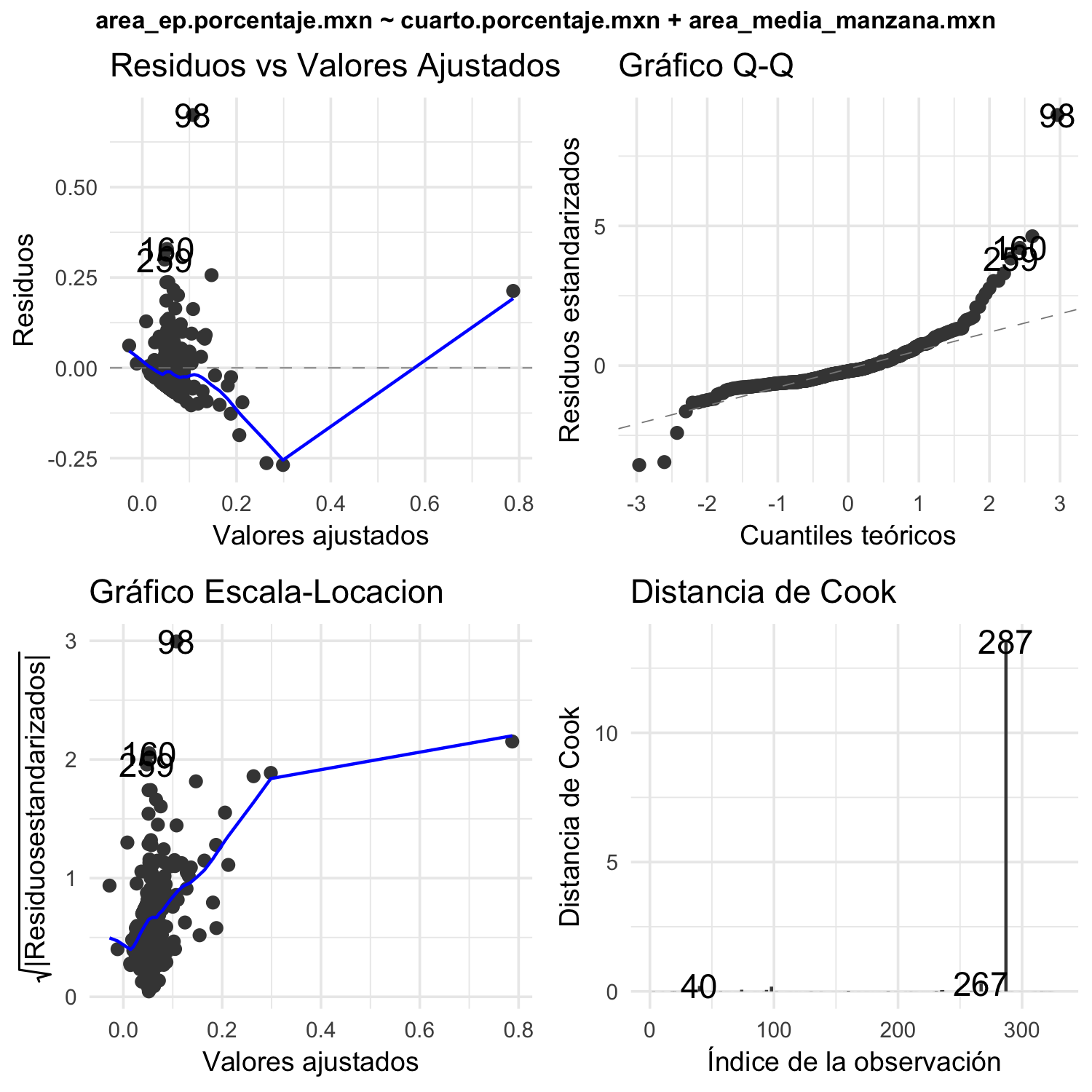
Figura 4.25: Gráficas diagnósticas para OLS del porcentaje de EV

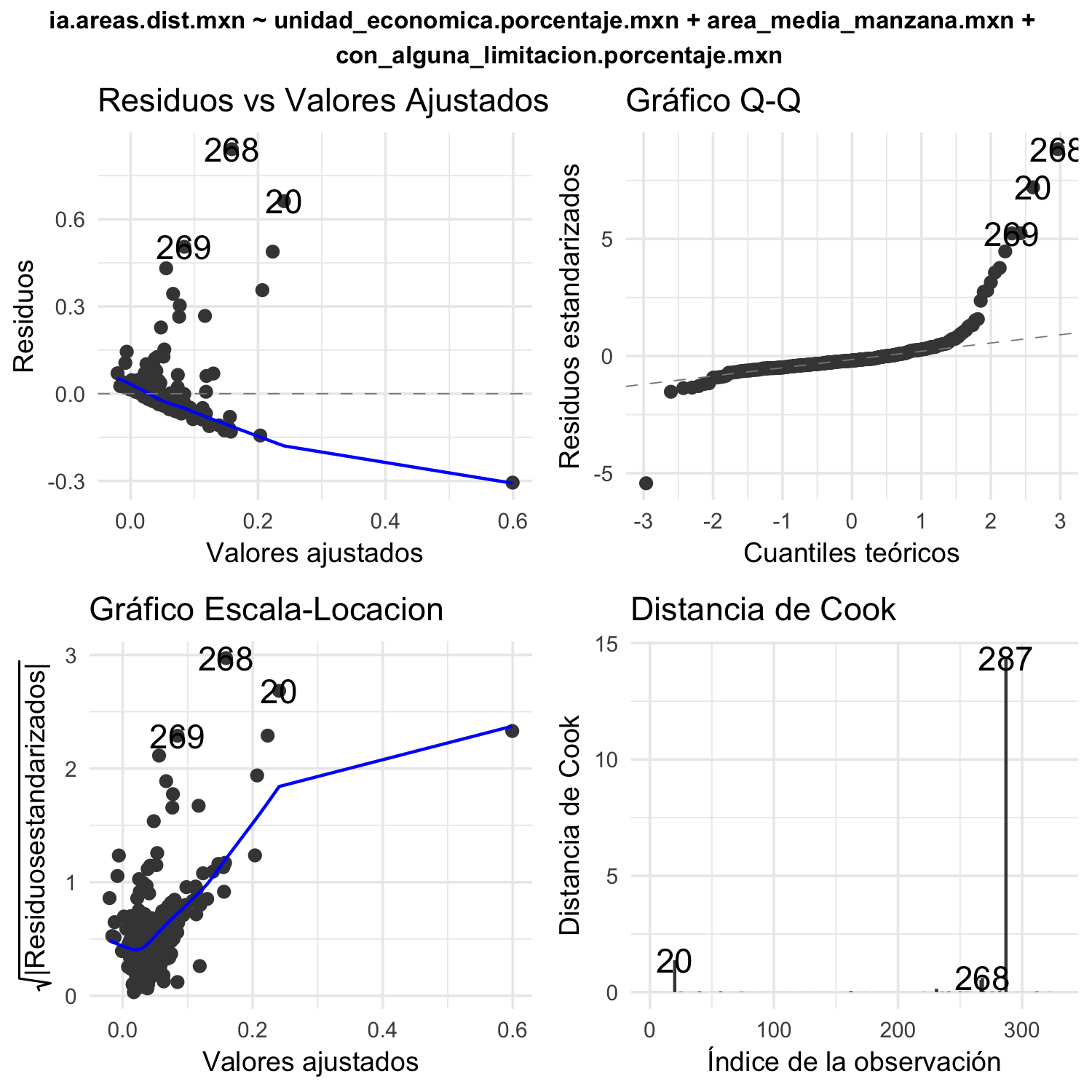
Figura 4.26: Gráficas diagnósticas para OLS de índice área-distancia

4.2.3 Modelado espacial de espacios verdes

El proceso de ajuste de los modelos geoestadísticos para el análisis de espacios verdes hace uso de los mismos elementos metodológicos usados para la cobertura de copa. Se usaron las dos matrices de vecindad usando un kernel de vecindad Queen $W_q$ y otro con base en un radio de búsqueda de 1 kilómetro $W_d$ usadas en el análisis del AU (ver figura 4.9).

4.2.3.1 Autocorrelación variables dependientes

Se analizó la autocorrelación de las variables dependientes para encontrar agrupaciones existentes en los datos que pueden ser explicados por la estructura de vecindad. Los resultados de los test de Moran’I para ambas variables dependientes muestran que existen patrones de agrupamiento y puede rechazarse la hipótesis nula de que los procesos espaciales subyacentes son aleatorios (ver tablas 4.21 y 4.22).

Ambos diseños de matriz revelan presencia clara de autocorrelación espacial. La matriz $W_q$ captura mejor la autocorrelación de ambos indicadores. El indicador razón área-distancia exhibe un valor de autocorrelación mucho más alto que área de EV [%]. El cálculo del índice razón área-distancia en su construcción usa una distancia de radio de búsqueda de 1 kilómetro. En su definición el indicador está influenciado por sus vecinos por lo que se forman grupos o clusters alrededor de ciertos sectores urbanos. Resulta pues interesante no sea $W_d$ la que capture mejor el agrupamiento.

Los mapas LISA para ambos indicadores de acceso a EV usando la matriz $W_q$ muestran los grupos de sectores autocorrelacionados (figuras 4.27 y 4.28). Los grupos formados muestran agrupaciones de alto acceso a EV en relación al resto de la ciudad. Se aprecia que se forman clusters alrededor de cuatro zonas en el caso del porcentaje de área de EV y dos para el indicador de relación áreas-distancia, coincidentes con el anterior. Esos sectores albergan equipamientos de ciudad como un cementerio de gran tamaño, las universidades y zonas conservadas de riberas de ríos. El grupo que se forma al oriente de la ciudad es donde se encuentra la laguna del Pondaje.

Tabla 4.21: Test de Moran - Porcenatje de EV para $W_q$ y $W_d$
	$W_q$	$W_d$
Estadístico Moran I	0.10462	0.05377
Expectativa	-0.00305	-0.00308
Varianza	0.00101	0.00076
Desviación estándar de Moran I	3.39376	2.06018
p-valor	0.00034	0.01969

Tabla 4.22: Test de Moran - Razón área distancia para $W_{q}$ y $W_{d}$
	$W_{q}$	$W_{d}$
Estadístico Moran I	0.78314	0.67779
Expectativa	-0.00305	-0.00308
Varianza	0.00102	0.00077
Desviación estándar de Moran I	24.62379	24.51886
p-valor	0.00000	0.00000

$Mapas LISA para la matriz $W_q$ de área de EV [\%]$

Figura 4.27: Mapas LISA para la matriz $W_q$ de área de EV [%]

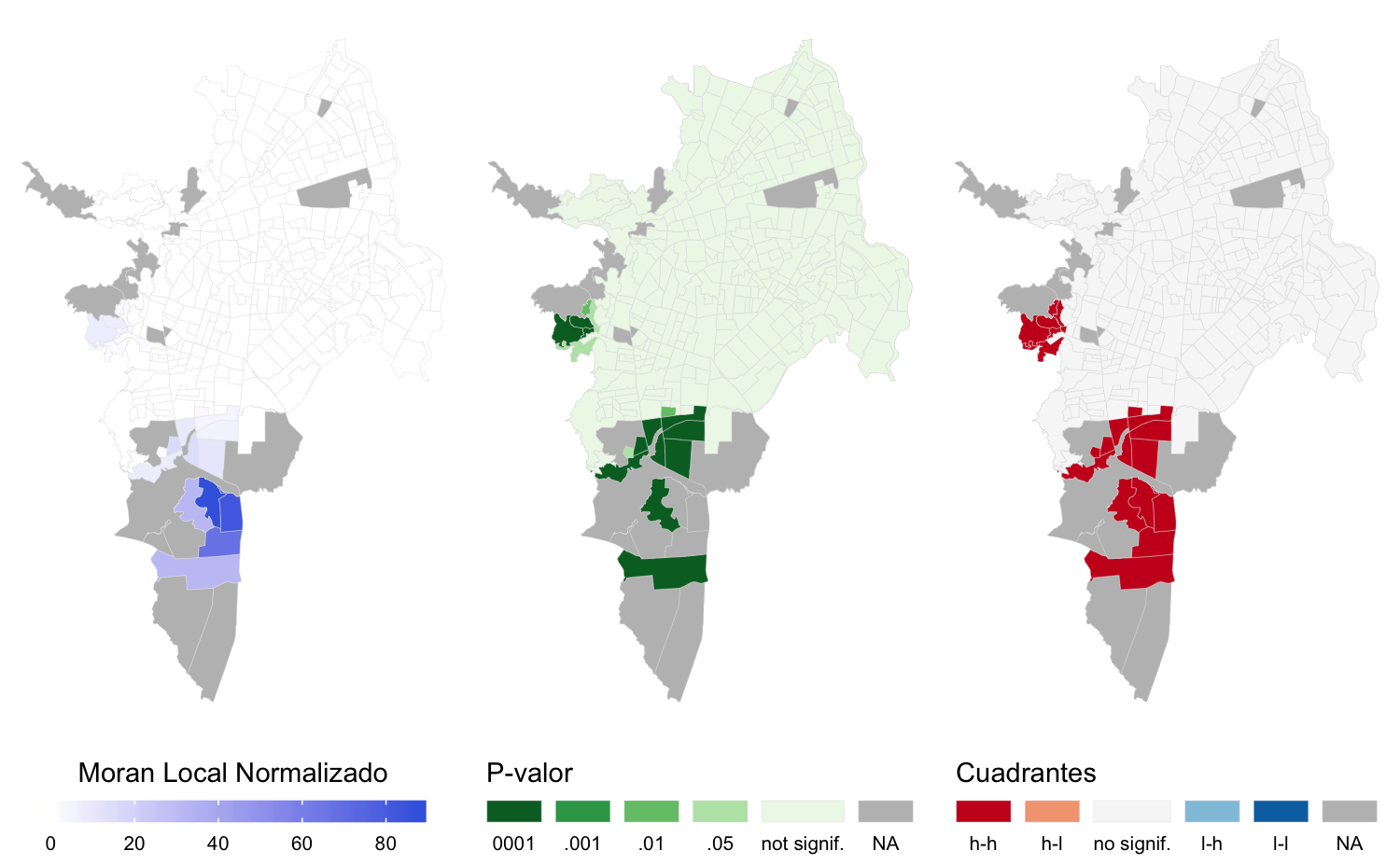
Figura 4.28: Mapas LISA para la matriz $W_q$ de razón área-distancia

4.2.3.2 Autocorrelación residuos de los OLS

La tabla 4.23 muestra que ambos diseños de matriz $W$ presentan un valor de Moran Global mayor que 0 y significativo para los residuos del OLS del porcentaje de área de EV, al igual que para los residuos del OLS del indicador áreas-distancia (ver tabla 4.24).

En ambos modelos el resultado de autocorrelación espacial sugiere que, al introducir retardos espaciales y la estructura de vecindad, pueden mejorar la estimación de los coeficientes de la regresión y las métricas de desempeño del ajuste.

Tabla 4.23: Test de Moran - Residuos de OLS Porcentaje EV $W_q$ y $W_d$
	$W_q$	$W_d$
Estadístico Moran I	0.11636	0.04201
Expectativa	-0.00305	-0.00308
Varianza	0.00108	0.00082
Desviación estándar de Moran I	3.63225	1.57642
p-valor	0.00014	0.05746

Tabla 4.24: Test de Moran - Residuos de OLS relación áreas distancias para $W_q$ y $W_d$
	$W_q$	$W_d$
Estadístico Moran I	0.61445	0.58256
Expectativa	-0.00305	-0.00308
Varianza	0.00105	0.00080
Desviación estándar de Moran I	19.04546	20.76452
p-valor	0.00000	0.00000

4.2.3.3 Modelo espacial porcentaje de espacio verde

Dado que la matriz $W_q$ capturó mejor la asociación espacial en los datos para ambos indicadores de acceso a EV, se realizó el ajuste de los modelos espaciales solo con ese diseño.

Las métricas de ajuste de los modelos de porcentaje de área de EV (ver tabla 4.25) muestran que los modelos espaciales logran eliminar la autocorrelación espacial global en los residuos. Todos los modelos mejoran las métricas de error respecto del OLS y ninguno logra la normalidad ni la homocedasticidad en los residuos.

Al comparar los resultados usando el desempeño en AIC se identificó al modelo SEM con el mejor ajuste. El modelo SEM logra eliminar la autocorrelación espacial global en los residuos. El coeficiente $\lambda$ del término autorregresivos es alto y significativo (tabla 4.27), lo que sugiere que no es necesario plantear efectos de la variables dependientes rezagadas, y que es posible que ese efecto sea por otras variables no tenidas en cuenta. Esta lectura del SEM es interesante y consistente con el significado local del indicador porcentaje de área de EV.

El resultado del modelo SEM confirma la significancia y efecto positivo para el acceso EV del área de promedio de la manzana en un SU. La presencia de viviendas tipo cuarto, con coeficiente negativos, es un factor que coincide con la disminución de área de EV disponible (ver tabla 4.26). Existen cambios y ajustes en los valores de los coeficientes con relación al modelo OLS, que dadas las mejoras en las métricas de ajuste hacen más confiables las estimaciones.

Tabla 4.25: Metricas de ajuste para los modelos de porcentaje de área de EV con $W_q$
medidasfit	OLS	SAR	SEM	SD
Globla Moran’I	0.11636	0.04015	-0.00817	-0.00602
GMI p-value	0.00014	0.09378	0.56220	0.53618
Shapiro-Wilk	0.76782	0.76040	0.75813	0.76159
SW p-value	0.00000	0.00000	0.00000	0.00000
Breusch-Pagan	12.98572	13.97239	11.07822	13.54161
BP p-value	0.00151	0.00092	0.00393	0.00891
Media Residuos	0.00000	0.00000	0.00000	0.00000
MSE	0.00607	0.00596	0.00581	0.00576
adj-Rsquare	0.29656	NA	NA	NA
Nagelkerke pseudo-R-squared	NA	0.31043	0.32222	0.32798
AIC	-737.84913	-740.39306	-746.06370	-744.87233
Log likelihood	372.92456	375.19653	378.03185	379.43617

Tabla 4.26: Coeficientes del modelo SEM de porcentaje de área de EV
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	0.049	0.007	7.116	0.000
vivienda tipo cuarto [%]	-0.098	0.042	-2.355	0.019
área media de manzana	0.771	0.065	11.803	0.000

Tabla 4.27: Coeficiente de autocorrelación modelo SEM de porcentaje de área de EV
$\lambda$	Likelihood ratio	p-valor
0.259	10.215	0.001

4.2.3.4 Modelo espacial del índice de acceso área-distancia

Las métricas de ajuste de los modelos de indicador área-distancia (ver tabla 4.28) muestran que los modelos espaciales logran eliminar la autocorrelación espacial global en los residuos. Todos los modelos mejoran las métricas de error respecto del OLS, en particular el Nagelkerke, equivalente al adj-Rsquare, que mide el nivel explicativo del modelo en la variabilidad de los datos, subiendo de $\simeq 0.17$ a $\simeq 0.74$.

Al comparar los resultados usando el desempeño en AIC se identificó al modelo SD con el mejor ajuste. El modelo SD logra eliminar la autocorrelación espacial global en los residuos. El coeficiente $\rho$ del término autorregresivos es muy alto y significativo (tabla 4.30), lo que sugiere que los efectos de las variables dependientes rezagadas son significativos. Existen cambios y ajustes en los valores de los coeficientes con relación al modelo OLS, que dadas las mejoras en las métricas de ajuste hacen más confiables las estimaciones (y se corrobora con las gráficas diagnósticas de la figura 4.29).

El resultado del modelo SD confirmó la significancia y efecto positivo pero bajo en el acceso a EV de contar con unidades económicas dentro del SU. Es significativo y fuerte en el acceso a EV estar al rededor de SUs con manzanas de área promedio grande. Por otro lado se desestima que exista una relación con la variable porcentaje personas con alguna limitación (ver tabla 4.29). La escogencia del modelo SD se ajusta consistentemente con el propósito del indicador áreas-distancia de medir el acceso en un SU más allá de su límite geográfico.

Tabla 4.28: Metricas de ajuste para los modelos de áreas-distancia de EV
medidasfit	OLS	SAR	SEM	SD
Globla Moran’I	0.61445	-0.17676	-0.17439	-0.13656
GMI p-value	0.00000	1.00000	1.00000	0.99998
Shapiro-Wilk	0.55302	0.50369	0.49323	0.59974
SW p-value	0.00000	0.00000	0.00000	0.00000
Breusch-Pagan	51.60213	15.79282	5.19151	73.10115
BP p-value	0.00000	0.00125	0.15830	0.00000
Media Residuos	0.00000	0.00000	0.00000	0.00000
MSE	0.00923	0.00279	0.00275	0.00252
adj-Rsquare	0.17542	NA	NA	NA
Nagelkerke pseudo-R-squared	NA	0.70286	0.70042	0.74346
AIC	-597.63015	-928.40318	-925.72082	-970.74368
Log likelihood	303.81507	470.20159	468.86041	494.37184

Tabla 4.29: Coeficientes del modelo SD índice de relación área distancia de EV
Término	Estimado	Error std.	t-valor	Pr(>\|t\|)
Intercepto	-0.027	0.017	-1.626	0.104
uso de unidad económica [%]	0.067	0.028	2.429	0.015
área media de manzana	0.015	0.048	0.314	0.754
con alguna limitación [%]	-0.030	0.022	-1.333	0.183
uso de unidad económica [%] (retardada)	-0.038	0.037	-1.036	0.300
área media de manzana (retardada)	0.694	0.101	6.870	0.000
con alguna limitación [%] (retardada)	0.063	0.035	1.786	0.074

Tabla 4.30: Coeficiente de autocorrelación modelo SD índice de relación área distancia de EV
$\rho$	Likelihood ratio	p-valor
0.747	255.817	0

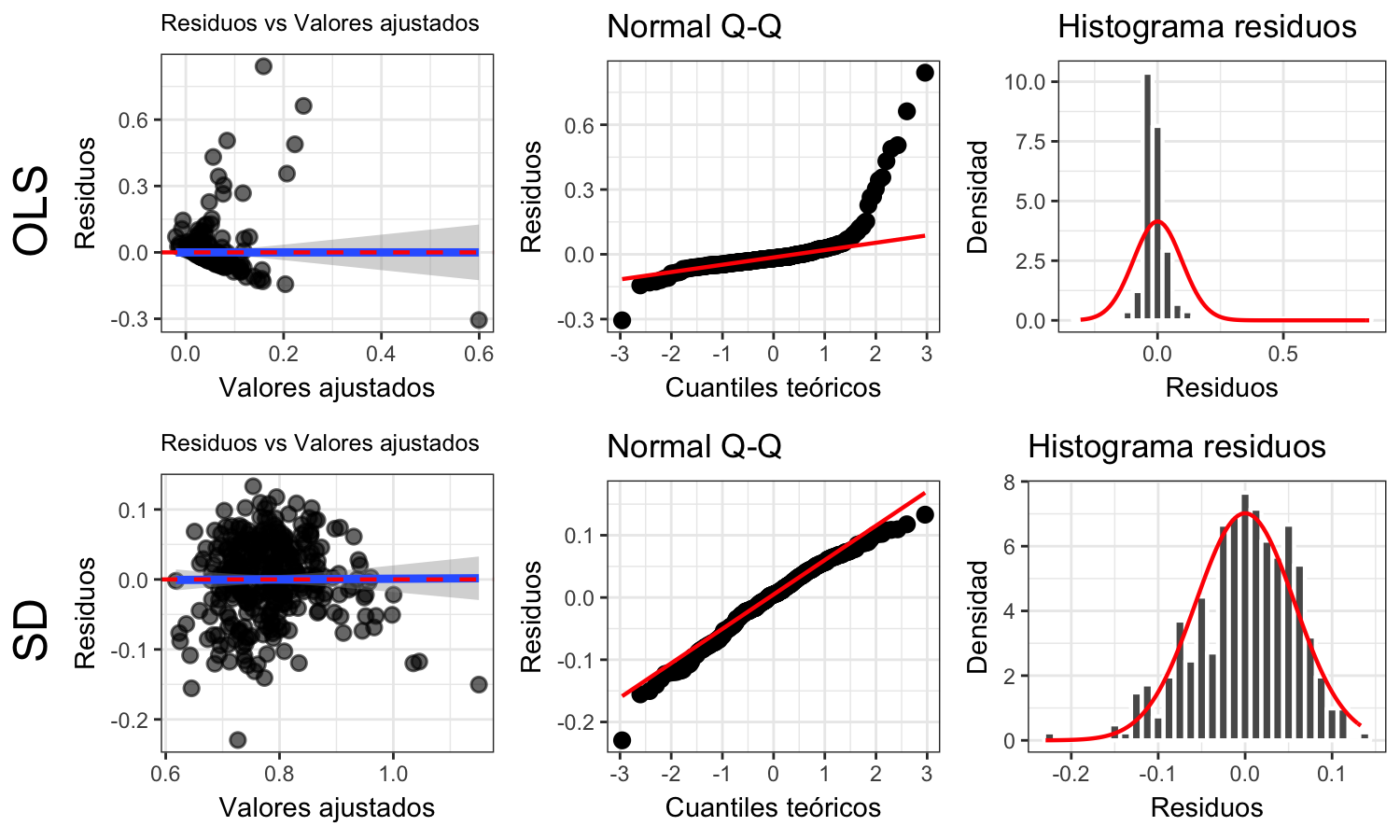
Figura 4.29: Diagnóstico comparativo entre modelos espaciales del indicador área-distancia